Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
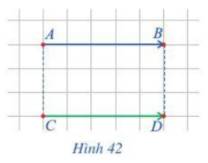
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.

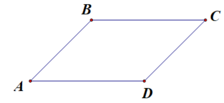
Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.

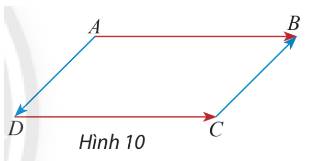
a) Ta có: \(AB = CD \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
\(AB//CD\) và \(\overrightarrow {AB} \), \(\overrightarrow {DC} \) có hướng từ trái sang phải
Suy ra \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
b) Ta có: \(AD = CB \Rightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|\)
\(AD//CB\) và \(\overrightarrow {AD} \)có hướng từ trên xuống dưới, \(\overrightarrow {CB} \) có hướng từ dưới lên trên. Suy ra \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \) ngược hướng

Về độ dài: hai vectơ AB→ và CD→ có cùng độ dài
Về hướng: hai vectơ AB→ và CD→ có hướng ngược nhau.

Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.

Ta có: giá của \(\overrightarrow {AB} \) là đường thẳng AB, giá của \(\overrightarrow {CD} \)là đường thẳng CD, và thấy rằng 2 đường thẳng này trùng nhau suy ra giá của 2 vecto này trùng nhau.
Tương tự ta thấy giá của cặp \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \) song song với nhau.

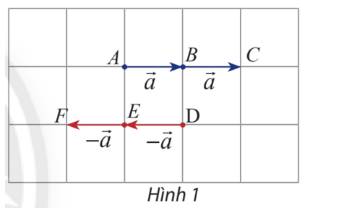
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)

Tham khảo:
\(\overrightarrow {CD} = \overrightarrow {BA} \) do hai vectơ \(\overrightarrow {CD} ,\;\overrightarrow {BA} \) cùng hướng và \(CD = BA\).
\(\begin{array}{l} \Rightarrow \overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} \\ \Leftrightarrow \left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {CA} } \right| = CA\end{array}\)
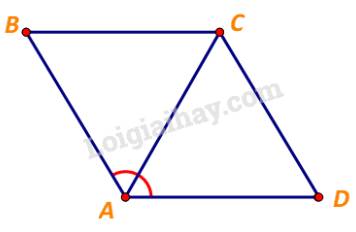
Xét tam giác ABC, ta có:
\(BA = BC\) và \(\widehat {BAC} = \frac{1}{2}.\widehat {BAD} = {60^o}\)
\( \Rightarrow \Delta ABC\) đều, hay \(CA = BC = 1\)
Vậy \(\left| {\overrightarrow {CB} + \overrightarrow {CD} } \right| = 1.\)
Dựa vào tính chất kết hợp, ta có:
\(\begin{array}{l}\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} = \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) + \overrightarrow {BA} \\ = \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right) + \overrightarrow {BA} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} .\\ \Rightarrow \left| {\overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {BA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = 1.\end{array}\)

Tham khảo:

Ta có: \( \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (do ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {BM} = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\( \Rightarrow \) Tứ giác ABMC là hình bình hành.
\( \Rightarrow \overrightarrow {DC} =\overrightarrow {AB} = \overrightarrow {CM} \).
\( \Rightarrow C\) là trung điểm DM.
Vậy M thuộc DC sao cho C là trung điểm DM.
Chú ý khi giải
+) Tứ giác ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
+) ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)


\(\overrightarrow{AB}=\overrightarrow{CD}\)