
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

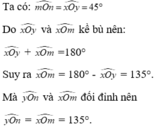

\(a)\) 4 góc có đỉnh \(O:\)
\(\widehat{xoy};\widehat{x'oy};\widehat{x'oy'};\widehat{xoy'}\)
\(b,\)
\(\widehat{xoy}=55^o\)
\(\widehat{xoy'}=125^o\)
\(\widehat{x'oy'}=55^o\)
\(\widehat{x'oy}=125^o\)
Trong 4 góc này thì :
\(+)\) 2 góc nhọn :\(\widehat{xoy};\widehat{x'oy'}\)
\(+)\) 2 góc tù : \(\widehat{x'oy};\widehat{xoy'}\)

a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOz}< \widehat{xOy}\left(35^0< 76^0\right)\)
nên tia Oz nằm giữa hai tia Ox và Oy
\(\Leftrightarrow\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{yOz}=\widehat{xOy}-\widehat{xOz}=76^0-35^0\)
hay \(\widehat{yOz}=41^0\)
Vậy: \(\widehat{yOz}=41^0\)

a) trên nữa mp bờ chứa tia ox ta có xot<xoy(30<60)
⇒ot nằm giữa 2 tia còn lại
⇒ xot + toy = xoy
30 độ + toy = 60 độ
toy = 60 độ - 30 độ = 30 độ
b) vì ox' và ox 2 là tia đối
⇒ tia x'oy và xoy là 2 góc kề bù
⇒ x'oy + xoy = 180
x'oy + 60 độ = 180 độ
x'oy = 180 độ - 60 độ = 120 độ
vì oy và oy' là 2 tia đối nhau
⇒ x'oy và x'oy' là 2 góc kề bù
⇒ x'oy + x'oy' = 180 độ
120 độ + x'oy' = 180 độ
x'oy' = 180 độ = 120 độ = 60 độ
vậy x'oy' = 60 độ
Ta có: \(\widehat{xOy}=\widehat{x'Oy'}\)(Hai góc đối đỉnh)
mà \(\widehat{xOy}=60^0\)
nên \(\widehat{x'Oy'}=60^0\)
Vậy: \(\widehat{x'Oy'}=60^0\)

a) Ta có góc xOy+x'Oy=180 độ ( 2 góc kề bù)
suy ra 60 độ +x'Oy=180 độ
x'Oy=180 độ -60 độ
x'Oy=120 độ
b)ta có tOy=\(\dfrac{1}{2}\)xOY (Ot là tia pg của góc xOy)
tOy=\(\dfrac{1}{2}\) 60 độ
tOy=30 độ
Ta có zOy=\(\dfrac{1}{2}\)x'Oy ( Oz là tia pg của góc x'Oy)
zOy=\(\dfrac{1}{2}\) 120 dộ
zOy=60 độ
Ta có tOy+zOy=zOt
30 độ+60=zOt
zOt=90 độ
Vậy zOt=90 độ

a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(40^0< 110^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz

b) Ta có: tia Om là tia phân giác của \(\widehat{xOy}\)(gt)
nên \(\widehat{xOm}=\dfrac{\widehat{xOy}}{2}=\dfrac{60^0}{2}=30^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOm}< \widehat{xOz}\left(30^0< 120^0\right)\)
nên tia Om nằm giữa hai tia Ox và Oz
\(\Leftrightarrow\widehat{xOm}+\widehat{mOz}=\widehat{xOz}\)
\(\Leftrightarrow\widehat{mOz}=\widehat{xOz}-\widehat{xOm}=120^0-30^0=90^0\)
Vậy: \(\widehat{mOz}=90^0\)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(60^0< 120^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
\(\Leftrightarrow\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
\(\Leftrightarrow\widehat{yOz}+60^0=120^0\)
hay \(\widehat{yOz}=60^0\)
Ta có: tia Oy nằm giữa hai tia Ox và Oz(cmt)
mà \(\widehat{xOy}=\widehat{yOz}\left(=60^0\right)\)
nên Oy là tia phân giác của \(\widehat{xOz}\)(đpcm)