Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

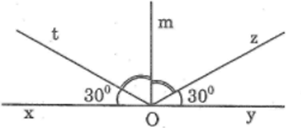
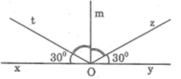
a, b, c, d Hình vẽ:
e) Vì Om là tia phân giác của ∠tOz nên tia Om nằm giữa tia Ot và tia Oz và ∠tOm = ∠mOz.
Vì tia Ot nằm giữa tia Ox và tia Om nên ∠xOm = ∠xOt + ∠tOm.
Tia Oz nằm giữa tia Om và tia Oy nên ∠yOm = ∠yOz + ∠zOm.
Mà ∠xOt = ∠yOz(= 30o); ∠tOm = ∠mOz
Do đó ∠xOm = ∠mOy mà hai góc đó kề nhau.
Suy ra Om cũng là tia phân giác của góc ∠xOy. ok bn

1)
a) ta có zOx kề bù với yOz => xOz=180-yOz=180-60=120
b) Om, On lần lượt là pg của xOy là sao?
2)
a) tương tự câu a bài 1
b) góc mOt và góc nOt có kề nhau vì có cạnh Ot chung
ta có: góc Om là pg của yOt=> góc mOt=1/2 yOt=1/2 60=30
On là pg của tOx => tOn= 1/2 120=60
=> góc mOt+tOn=60+30=90 => 2 góc này có phụ nhau

a) Ta có: \(\widehat{xOz}+\widehat{yOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{yOz}+60^0=180^0\)
hay \(\widehat{yOz}=120^0\)
b) Ta có: \(\widehat{xOt}+\widehat{tOy}=180^0\)
\(\Leftrightarrow\widehat{tOy}+\dfrac{\widehat{xOz}}{2}=180^0\)
\(\Leftrightarrow\widehat{tOy}=120^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOz}< \widehat{yOt}\left(60^0< 120^0\right)\)
nên tia Oz nằm giữa hai tia Oy và Ot
mà \(\widehat{yOz}=\dfrac{1}{2}\widehat{yOt}\left(60^0=\dfrac{1}{2}\cdot120^0\right)\)
nên Oz là tia phân giác của \(\widehat{yOt}\)

a) Ta có: \(\widehat{yOz}+\widehat{zOx}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xOz}+60^0=180^0\)
hay \(\widehat{xOz}=120^0\)

x O y t z m