Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

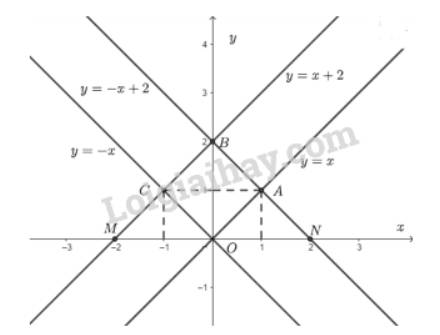
- Vẽ đồ thị hàm số \(y = x\)
Cho \(x = 1 \Rightarrow y = 1\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;1} \right)\).
Đồ thị hàm số \(y = x\)là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Vẽ đồ thị hàm số \(y = x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(B\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = - 2\) ta được điểm \(M\left( { - 2;0} \right)\) trên \(Ox\).
Đồ thị hàm số\(y = x + 2\)là đường thẳng đi qua hai điểm \(B\left( {0;2} \right)\) và \(M\left( { - 2;0} \right)\).
- Vẽ đồ thị hàm số \(y = - x\)
Cho \(x = 1 \Rightarrow y = - 1\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(C\left( {1; - 1} \right)\).
Đồ thị hàm số \(y = - x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(C\left( {1; - 1} \right)\).
- Vẽ đồ thị hàm số \(y = - x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(B\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = 2\) ta được điểm \(N\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = - x + 2\) là đường thẳng đi qua hai điểm \(B\left( {0;2} \right)\) và \(N\left( {2;0} \right)\).

+) Hàm số \(y=\frac{1}{2}x+2\)
\(x=0\Rightarrow y=2\)\(\Rightarrow A\left(0;2\right)\)
\(y=0\Rightarrow x=-4\)\(\Rightarrow B\left(-4;0\right)\)
Đồ thị hàm số \(y=\frac{1}{2}x+2\)là đường thẳng đi qua 2 điểm \(A\left(0;2\right)\)và \(B\left(-4;0\right)\)
+) Hàm số y = -x + 2
\(x=0\Rightarrow y=2\)\(\Rightarrow A\left(0;2\right)\)
\(y=0\Rightarrow x=2\)\(\Rightarrow D\left(2;0\right)\)
Đồ thị hàm số y = -x + 2 là đường thẳng đi qua 2 điểm \(A\left(0;2\right)\)và \(D\left(2;0\right)\)

a) * Vẽ đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Cho x = 0 thì y = 3, ta được điểm P(0; 3) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Cho y = 0 thì x = 6 ta được điểm A(6; 0) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Vậy đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\) là đường thẳng đi qua hai điểm P(0; 3) và điểm A(6; 0).
* Vẽ đồ thị hàm số y = 2x – 2
Cho x = 0 thì y = -2 ta được điểm Q(0; -2) thuộc đồ thị hàm số y = 2x – 2
Cho y = 0 thì x = 1 ta được điểm B(1; 0) thuộc đồ thị hàm số y = 2x -2
Vậy đồ thị hàm số y = 2x – 2 là đường thẳng đi qua hai điểm Q(0; -2) và B(1; 0)
b) Ta có: A là giao điểm của đường thẳng \(y = - \dfrac{1}{2}x + 3\) với trục hoành nên \( - \dfrac{1}{2}x + 3 = 0\) suy ra x = 6 nên A(6; 0)
Ta có: B là giao điểm của đường thẳng y = 2x – 2 với trục hoành nên 2x – 2 = 0 suy ra x = 1 nên B(1; 0)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(y = - \dfrac{1}{2}x + 3\) và y = 2x – 2 ta có:
\(\begin{array}{l} - \dfrac{1}{2}x + 3 = 2{\rm{x}} - 2\\ \Rightarrow 3 + 2 = \dfrac{1}{2}x + 2{\rm{x}}\\ \Rightarrow 5 = \dfrac{5}{2}x\\ \Rightarrow x = 2 \Rightarrow y = 2\end{array}\)
Vì C là hoành độ giao điểm của hai đường thẳng \(y = - \dfrac{1}{2}x + 3\) và y = 2x – 2 nên C(2; 2)
Gọi H là hình chiếu của C lên trục Ox
Khi đó: CH = 2
Mặt khác AB = 5 cm
Diện tích tam giác ABC là; \({S_{ABC}} = \dfrac{1}{2}CH.AB = \dfrac{1}{2}.2.5 = 5\left( {c{m^2}} \right)\)

a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
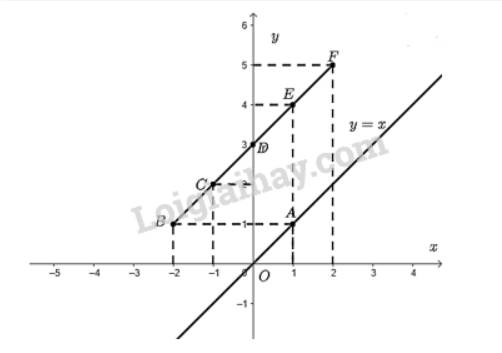
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).

b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+2\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1}{4}\cdot4^2=4\\y=\dfrac{1}{4}\cdot\left(-2\right)^2=1\end{matrix}\right.\)

\(a)\dfrac{{3{\rm{x}} + 6}}{{4{\rm{x}} - 8}}.\dfrac{{2{\rm{x}} - 4}}{{x + 2}} = \dfrac{{3\left( {x + 2} \right).2\left( {x - 2} \right)}}{{4.\left( {x - 2} \right).\left( {x + 2} \right)}} = \dfrac{3}{2}\)
\(b)\dfrac{{{x^2} - 36}}{{2{\rm{x}} + 10}}.\dfrac{{x + 5}}{{6 - x}} = \dfrac{{\left( {x - 6} \right)\left( {x + 6} \right)\left( {x + 5} \right)}}{{2\left( {x + 5} \right).\left( { - 1} \right)\left( {x - 6} \right)}} = \dfrac{{x + 6}}{{ - 2}} = \dfrac{{-x- 6}}{{ 2}}\)
\(c)\dfrac{{1 - {y^3}}}{{y + 1}}.\dfrac{{5y + 5}}{{{y^2} + y + 1}} = \dfrac{{\left( {1 - y} \right)\left( {1 + y + {y^2}} \right).5\left( {y + 1} \right)}}{{\left( {y + 1} \right).\left( {{y^2} + y + 1} \right)}} = 5\left( {1 - y} \right)\)
\(d)\dfrac{{x + 2y}}{{4{{\rm{x}}^2} - 4{\rm{x}}y + {y^2}}}.\left( {2{\rm{x}} - y} \right) = \dfrac{{\left( {x + 2y} \right).\left( {2{\rm{x}} - y} \right)}}{{{{\left( {2{\rm{x}} - y} \right)}^2}}} = \dfrac{{x + 2y}}{{2{\rm{x}} - y}}\)

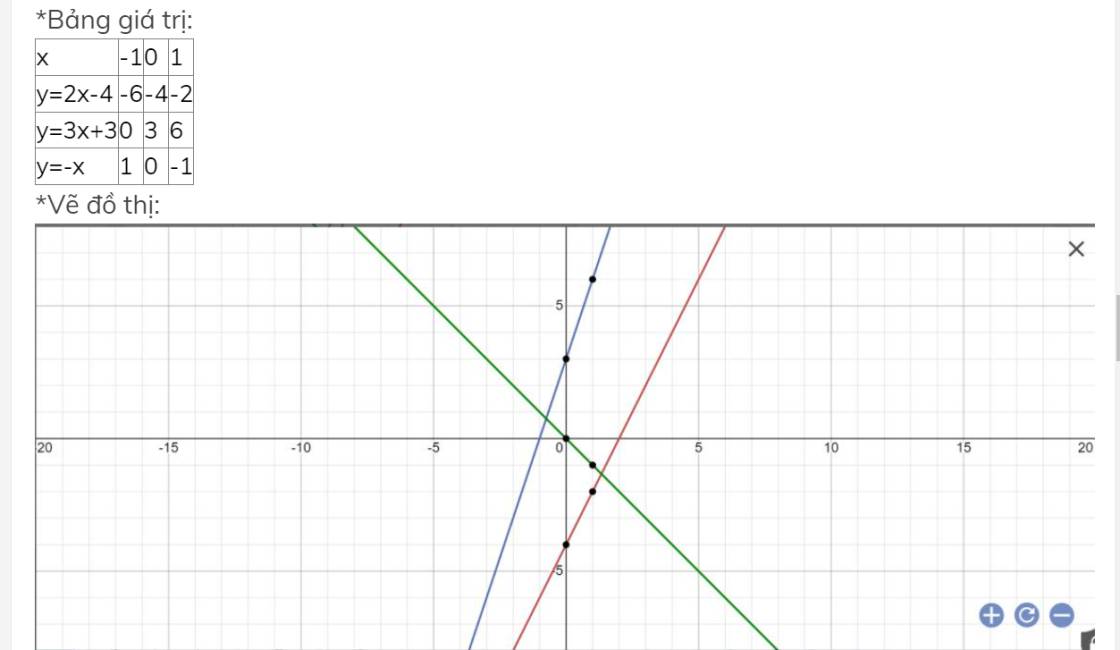
*Bảng giá trị:
| x | -1 | 0 | 1 |
| y=2x-4 | -6 | -4 | -2 |
| y=3x+3 | 0 | 3 | 6 |
| y=-x | 1 | 0 | -1 |
*Vẽ đồ thị:
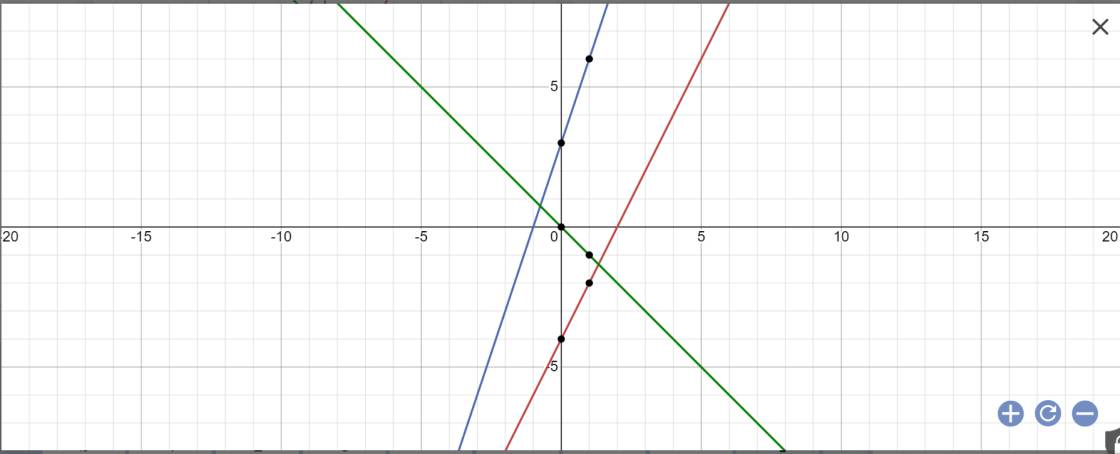

a:Đặt (d1): y=2x-3
Tọa độ giao điểm của (d1) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của (d1) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-3=0-3=-3\end{matrix}\right.\)
b: Đặt (d2): \(y=-\dfrac{3}{4}x\)
Tọa độ giao điểm của (d2) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{3}{4}x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của (d2) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{3}{4}x=-\dfrac{3}{4}\cdot0=0\end{matrix}\right.\)
c: Đặt \(\left(d3\right):y=2x^2\)
Tọa độ giao điểm của (d3) với trục Ox là:
\(\left\{{}\begin{matrix}2x^2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=0\\y=2x^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=2\cdot0^2=0\end{matrix}\right.\)
Tọa độ giao điểm của (d3) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0^2=0\end{matrix}\right.\)
d: Đặt (d4): \(y=\dfrac{x+1}{x-2}\)
ĐKXĐ: x<>2
Tọa độ giao điểm của (d4) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\y=\dfrac{x+1}{x-2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của (d4) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{x+1}{x-2}=\dfrac{0+1}{0-2}=\dfrac{1}{-2}=-\dfrac{1}{2}\end{matrix}\right.\)
e: Đặt (d5): \(y=x-2+\dfrac{1}{x}\)
ĐKXĐ: x<>0
Vì hàm số không đi qua điểm có hoành độ là x=0 nên (d5) sẽ không cắt trục Oy
Tọa độ giao điểm của (d5) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\x-2+\dfrac{1}{x}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-2x+1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x-1\right)^2=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
f: Đặt (d6): \(y=x^2+2x-5\)
Tọa độ giao điểm của (d6) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=x^2+2x-5=0^2+2\cdot0-5=-5\end{matrix}\right.\)
Tọa độ giao điểm của (d6) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\x^2+2x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x^2+2x+1-6=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\left(x+1\right)^2=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x+1=\sqrt{6}\end{matrix}\right.\\\left\{{}\begin{matrix}y=0\\x+1=-\sqrt{6}\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=\sqrt{6}-1\end{matrix}\right.\\\left\{{}\begin{matrix}y=0\\x=-\sqrt{6}-1\end{matrix}\right.\end{matrix}\right.\)

* y = 3x
Với x = 1 thì y = 3, ta được điểm A(1; 3) thuộc đồ thị hàm số y = 3x
Vậy đồ thị hàm số y = 3x là đường thẳng đi qua hai điểm O(0; 0) và A(1; 3)
* y = 3x + 4
Với x = 0 thì y = 4, ta được điểm B(0; 4) thuộc đồ thị hàm số y = 3x + 4
Với x = -1 thì y = 1, ta được điểm C(-1; 1) thuộc đồ thị hàm số y = 3x + 4
Vậy đồ thị hàm số y = 3x + 4 là đường thẳng đi qua hai điểm B(0; 4) và C(-1; 1)
* \(y = - \dfrac{1}{2}x\)
Với x = 2 thì y = -1, ta được điểm D(2; -1) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x\)
Vậy đồ thị hàm số \(y = - \dfrac{1}{2}x\) là đường thẳng đi qua hai điểm O(0; 0) và điểm D(2; -1)
* \(y = - \dfrac{1}{2}x + 3\)
Với x = 0 thì y = 3, ta được điểm E(0; 3) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Với y = 0 thì x = 6 ta được điểm H(6; 0) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Vậy đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\) là đường thẳng đi qua hai điểm E(0; 3) và H(6; 0)