Vẽ đồ thị biểu diễn diện tích hình tròn theo bán kính của nó

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

23 tháng 2 2018

Vẽ đồ thị biểu diễn diện tích hình tròn theo bán kính của nó

#Toán lớp 9

Cao Minh Tâm

23 tháng 2 2018

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Phạm Minh Dũng

21 tháng 5 2021

a) Vẽ đồ thị hàm số y = – 2x2 b) Cho đường tròn (O), đường kính AB; P (O) sao cho (Hình 3). Tính số đo c) Một hình trụ có chiều cao bằng 12 cm và diện tích xung quanh là 96 cm2. Hãy tính bán kính của đường tròn đáy đó? ...

Đọc tiếp

#Toán lớp 9

Akai Haruma

Giáo viên

22 tháng 5 2021

Bạn chịu khó gõ đề chay (viết nguyên chữ thôi, những chỗ cần công thức thì mở hộp $\sum$, không chèn hình, không chèn ký hiệu khác ngoài) để bài dễ nhìn hơn, nâng cao khả năng hỗ trợ giải bài.

Bài như này nhìn rất "khó chịu" (hình minh họa bên dưới)

Đúng(0)

Sách Giáo Khoa

9 tháng 5 2017

a) Điền vào ô trống trong bảng sau (S là diện tích hình tròn bán kính R) R 0 1 2 3 4 5 10 20 S b) Vẽ đồ thị biểu diễn diện tích hình tròn theo bán kính của nó c) Diện tích hình tròn có tỉ lệ thuận với bán kính không...

Đọc tiếp

#Toán lớp 9

Nguyen Thuy Hoa

2 tháng 6 2017

Góc với đường tròn

Đúng(0)

Pham Trong Bach

20 tháng 9 2018

Diện tích S của hình tròn được tính bởi công thức S = πR2, trong đó R là bán kính của hình tròn.

Tính bán kính của hình tròn, làm tròn kết quả đến chữ số thập phân thứ hai, nếu biết diện tích của nó bằng 79,5 cm2.

#Toán lớp 9

Cao Minh Tâm

20 tháng 9 2018

Diện tích hình tròn bằng 79,5

Giải bài 1 trang 30 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng(0)

Pham Trong Bach

6 tháng 1 2018

Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:

Hình tròn bán kính R (ứng với cung 360o) có diện tích là … .

Vậy hình quạt tròn bán kính R, cung 1o có diện tích là … .

Hình quạt tròn bán kính R, cung no có diện tích S = … .

#Toán lớp 9

Cao Minh Tâm

6 tháng 1 2018

Hình tròn bán kính R (ứng với cung 360o) có diện tích là πR2

Vậy hình quạt tròn bán kính R, cung 1o có diện tích là (πR2)/360

Hình quạt tròn bán kính R, cung no có diện tích S = (πR2n)/360

Đúng(0)

Pham Trong Bach

20 tháng 8 2017

Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:

Hình tròn bán kính R (ứng với cung 360 ° ) có diện tích là … .

Vậy hình quạt tròn bán kính R, cung 1 ° có diện tích là … .

Hình quạt tròn bán kính R, cung n ° có diện tích S = … .

#Toán lớp 9

Cao Minh Tâm

20 tháng 8 2017

Hình tròn bán kính R (ứng với cung 360 ° ) có diện tích là π R 2

Vậy hình quạt tròn bán kính R, cung 1 ° có diện tích là π R 2 / 360

Hình quạt tròn bán kính R, cung n ° có diện tích S = π R 2 n / 360

Đúng(0)

Tuyen Huynh

3 tháng 9 2016 - olm

cho đường tròn tâm o bán kính r, đường kính AB vẽ dây AM bằng r

a) Tính các góc tam giác AMB và MB theo r

b) Vẽ tia phân giác MD của tam giác AMB .Gọi E,F là chân đường vuông góc vẽ từ D đến MA,MB .Tứ giác MEDF là hình gì ?vì sao? tính chu vi và diện tích của nó theo r

#Toán lớp 9

Pham Trong Bach

9 tháng 2 2019

Diện tích S của hình tròn được tính bởi công thức S = π R 2 , trong đó R là bán kính của hình tròn.a) Dùng máy tính bỏ túi, tính các giá trị của S rồi điền vào các ô trống trong bảng sau (π ≈ 3,14, làm tròn kết quả đến chữ số thập phân thứ hai). R (cm) 0,57 1,37 2,15 4,09 S = πR2 (Xem bài đọc thêm về máy tính bỏ túi dưới đây.)b) Nếu...

Đọc tiếp

#Toán lớp 9

Cao Minh Tâm

9 tháng 2 2019

a) (Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).

+ Nhập hàm số: Giải bài 1 trang 30 SGK Toán 9 Tập 2 | Giải toán lớp 9

+ Nhập giá trị:

Giải bài 1 trang 30 SGK Toán 9 Tập 2 | Giải toán lớp 9

Vậy ta có bảng sau:

R (cm)	0,57	1,37	2,15	4,09
S = πR2	1,02	5,9	14,52	52,55

b) Gọi bán kính mới là R’. Ta có R’ = 3R.

Diện tích mới là :

S ' = π R ' 2 = π ( 3 R ) 2 = π 9 R 2 = 9 π R 2 = 9 S

Vậy khi bán kính tăng lên 3 lần thì diện tích tăng 9 lần.

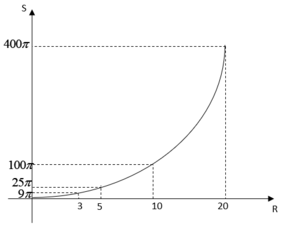
c) Diện tích hình tròn bằng 79,5

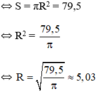
Giải bài 1 trang 30 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng(0)

Pham Trong Bach

16 tháng 11 2017

Diện tích xung quanh của một hình trụ là 10 m 2 và diện tích toàn phần của nó là 14 m 2 .Hãy tính bán kính của đường tròn đáy và chiều cao của hình trụ (lấy π =3,14 ; làm tròn kết quả đến chữ số thập phân thứ 2)

#Toán lớp 9

Cao Minh Tâm

16 tháng 11 2017

Diện tích toàn phần của hình trụ : S T P = S x q + 2 . S đ á y

Diện tích của một đáy :

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)

Black Magic

9 tháng 4 2020 - olm

Tính diện tích cạnh của hình tám cạnh đều theo bán kính R của đường tròn ngoại tiếp hình đó

#Toán lớp 9

Tran Le Khanh Linh

9 tháng 4 2020

Giả sử AB là 1 cạnh của hình tám cạnh đều, gọi AB=a.

Vẽ AK là đường co của tam giác OAB

Ta có: $\widehat{AOB}=\frac{360^o}{8}=45^o\Rightarrow OK=AK=\sin45^o=\frac{OA\sqrt{2}}{2}=\frac{R\sqrt{2}}{2}$

Nên KB=OB-OK=$\frac{R\sqrt{2}}{2}-R=R\left(\frac{\sqrt{2}}{2}-1\right)$

Xét tam giác KAB vuông tại K, theo định lý Pytago ta có:

$AB^2=AK^2+KB^2=\left(\frac{R\sqrt{2}}{2}\right)^2+\left[R\left(\frac{\sqrt{2}}{2}-1\right)\right]^2$

$AB^2=R^2\left(\frac{1}{2}+\frac{1}{2}-\sqrt{2}+1\right)$

$\Rightarrow AB^2=\left(2-\sqrt{2}\right)R^2$

$\Rightarrow AB=\sqrt{2-\sqrt{2}}R$

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP