K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 12 2021
Vì \(\Delta ABC\) vuông tại \(A\)
\(\Rightarrow\) \(AB , AC\) là hai cạnh góc vuông còn \(BC\) là cạnh huyền
Áp dụng định lý Py \(-\) ta \(-\) go vào \(\Delta ABC\) , ta có :
\(BC^2=AB^2+AC^2=3^2+4^2=9+16=25=5^2\)
\(\Rightarrow\) \(BC=5\)
Vậy \(BC = 5 cm\)
UP
0
PT
1
CM
30 tháng 1 2017
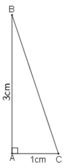
- Vẽ góc ∠ xAy = 90º
- Trên tia Ax lấy điểm B sao cho AB = 3cm.
Trên tia Ay lấy điểm C sao cho AC = 1cm.
- Nối các điểm B và C ta được tam giác ABC thỏa mãn.
Đo góc C ta được ∠C ≈ 72o.
4 tháng 3 2021
a) Vì tam giác ABC có AB=AC
=> ∆ABC cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\)
b) Ta có: \(\left\{{}\begin{matrix}\widehat{ABE}+\widehat{ABC}=180^o\\\widehat{ACD}+\widehat{ACD}=180^o\end{matrix}\right.\)
Mà \(\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{ABE}=\widehat{ACD}\)
Lại có: \(\widehat{EAB}+\widehat{BAC}=90^o\)
\(\widehat{DAC}+\widehat{CAB}=90^o\)
=> \(\widehat{EAB}=\widehat{DAC}\)
Xét ∆EAB và ∆DAC:
AB=AC(gt)
\(\widehat{EAB}=\widehat{DAC}\left(cmt\right)\)
\(\widehat{ABE}=\widehat{ACD}\left(cmt\right)\)
=> ∆EAB=∆DAC(g.c.g)
=> EB=CD(2 cạnh t/ứ)
=> EB+BC=DC+BC
=> EC=BD
=> Đpcm
4 tháng 3 2021
a) Xét ΔABC có AB=AC(gt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)
Giải đi