Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

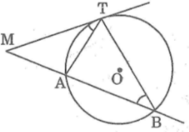

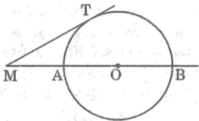
Vì cát tuyến MAB kẻ tùy ý nên ta luôn có M T 2 = MA.MB không phụ thuộc vị trí của cát tuyến MAB.

a: Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
DO đó: ΔMTA∼ΔMBT
Suy ra: MT/MB=MA/MT
hay \(MT^2=MA\cdot MB\)
b: MB=50cm
=>MA=8cm
=>AB=42cm
=>R=21cm

Gọi bán kính của đường tròn (O) là R
Ta có:MB=MA+AB = MA + 2R
Suy ra: MA =MB – 2R
Ta lại có: M T 2 = MA.MB (cmt)
Suy ra: M T 2 = (MB- 2R).MB = M B 2 – 2R.MB
![]()
a) Xét \(\Delta BMT\) và \(\Delta TMA\) có:
\(\widehat{M}\) chung
\(\widehat{B}=\widehat{MTA}\) (cùng chắn \(\stackrel\frown{AT}\))
\(\Rightarrow\Delta BMT\sim\Delta TMA\)
\(\Rightarrow\dfrac{MT}{MA}=\dfrac{MB}{MT}\Rightarrow MT^2=MA.MB\left(\text{Đ}PCM\right)\)