Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo bảng sau:

• Đối với khách hàng nam:
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {40;50} \right)\).
Do đó: \({u_m} = 40;{n_{m - 1}} = 6;{n_m} = 10;{n_{m + 1}} = 7;{u_{m + 1}} - {u_m} = 50 - 40 = 10\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 40 + \frac{{10 - 6}}{{\left( {10 - 6} \right) + \left( {10 - 7} \right)}}.10 = 45,7\)
Vậy ta có thể dự đoán khách hàng nam 46 tuổi có nhu cầu mua bảo hiểm nhiều nhất.
• Đối với khách hàng nữ:
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {30;40} \right)\).
Do đó: \({u_m} = 30;{n_{m - 1}} = 3;{n_m} = 9;{n_{m + 1}} = 6;{u_{m + 1}} - {u_m} = 40 - 30 = 10\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 30 + \frac{{9 - 3}}{{\left( {9 - 3} \right) + \left( {9 - 6} \right)}}.10 = 36,7\)
Vậy ta có thể dự đoán khách hàng nữ 37 tuổi có nhu cầu mua bảo hiểm nhiều nhất.

| Khoảng tuổi | [20;30) | [30;40) | [40;50) | [50;60) | [60;70) |
| Số khách | 3 | 9 | 6 | 4 | 2 |

a) Không thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh
b) Tần số lớn nhất là 16 nên nhóm chứa mốt là [5;10)
Ta có \(j = 2,\;{a_2} = 5,\;{m_2} = 16,\;{m_1} = 8;\;{m_3} = 4,\;h = 5.\) Do đó,
\({M_0} = 5 + \frac{{16 - 8}}{{\left( {16 - 8} \right) + \left( {16 - 4} \right)}} \times 5 = 7\).

Tần số lớn nhất là 31 nên nhóm chứa mốt là \(\left[ {60;80} \right).\;\)Ta có:
\(j = 4;\;\;{a_4} = 60;\;\;{m_4} = 31;\;\;{m_3} = 23;\;\;{m_5} = 29;\;\;h = 20\). Do đó,
\({M_0} = 60 + \frac{{31 - 23}}{{\left( {31 - 23} \right) + \left( {31 - 29} \right)}} \times 20 = 76\).
Ý nghĩa: Đa số các con ong có tuổi thọ là 76 ngày.

Tần số lớn nhất là 31
=>Nhóm chứa mốt là [60;80)
j=4
a4=60
m4=31; m3=23; m5=29; h=20
Do đó, ta có:
\(M_0=60+\dfrac{31-23}{\left(31-23\right)+\left(31-29\right)}\cdot20=76\)
=>Đa số các con ong có tuổi thọ là 76 ngày

Tham khảo:
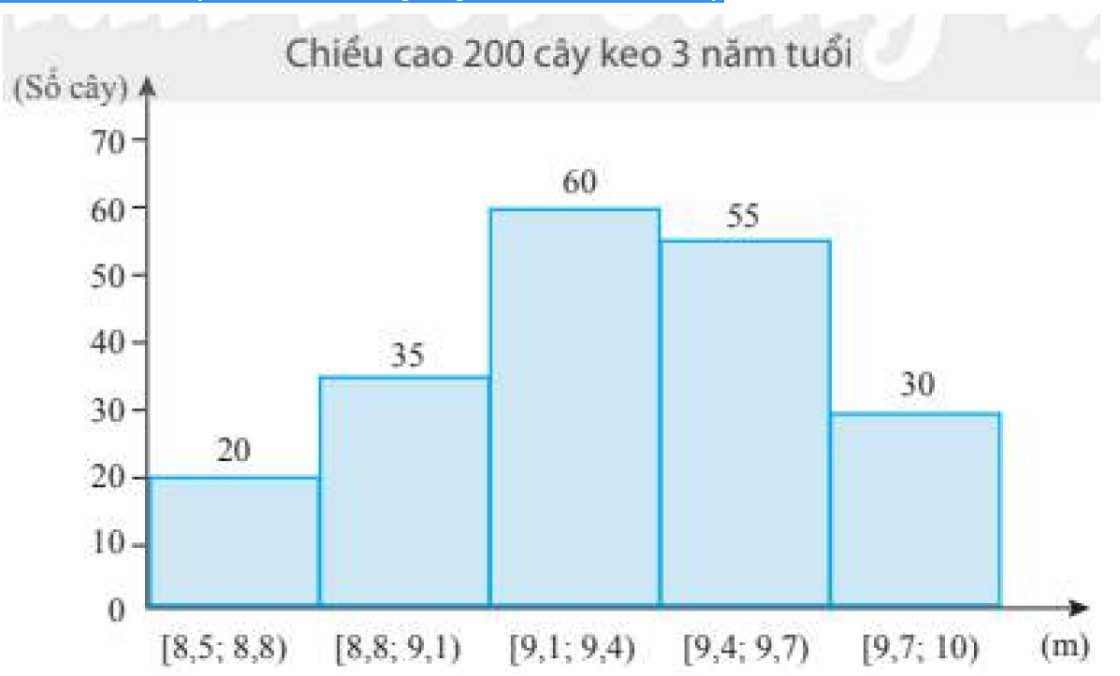
Chiều cao của 200 cây keo 3 năm tuổi được thống kê trong bảng sau:

Chiều cao của 200 cây keo 3 năm tuổi sau khi ghép nhóm là:
\(\bar x = \frac{{20.8,65 + 35.8,95 + 60.9,25 + 55.9,55 + 30.9,85}}{{200}} = 9,31\left( m \right)\)
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {9,1;9,4} \right)}\end{array}\).
Do đó: \({u_m} = 9,1;{n_{m - 1}} = 35;{n_m} = 60;{n_{m + 1}} = 55;{u_{m + 1}} - {u_m} = 9,4 - 9,1 = 0,3\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 9,1 + \frac{{60 - 35}}{{\left( {60 - 35} \right) + \left( {60 - 55} \right)}}.0,3 = 9,35\)
Vậy chiều cao của 200 cây keo 3 năm tuổi nhiều nhất là 9,35 mét.

a) Do số bệnh nhân là số nguyên nên ta hiệu chỉnh như sau:

Số bệnh nhân đến khám bệnh mỗi ngày trong tháng 4 năm 2022 là:
\(n = 7 + 8 + 7 + 6 + 2 = 30\).
Gọi \({x_1};{x_2};...;{x_{30}}\) là số bệnh nhân đến khám bệnh mỗi ngày được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_7} \in \begin{array}{*{20}{l}}{\left[ {0,5;10,5} \right)}\end{array};{x_8},...,{x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array};{x_{16}},...,{x_{22}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array};\\{x_{23}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{l}}{\left[ {40,5;50,5} \right)}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\)
Do \({x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array},{x_{16}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 20,5\).
• Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 30;{n_m} = 8;C = 7;{u_m} = 10,5;{u_{m + 1}} = 20,5\)
Do \({x_8} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{30}}{4} - 7}}{8}.\left( {20,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \({x_{23}}\).
Ta có: \(n = 30;{n_j} = 6;C = 7 + 8 + 7 = 22;{u_j} = 30,5;{u_{j + 1}} = 40,5\)
Do \({x_{23}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 30,5 + \frac{{\frac{{3.30}}{4} - 22}}{6}.\left( {40,5 - 30,5} \right) \approx 31,3\)
b) Do \({Q_3} \approx 31,3\) nên nhận định trên hợp lí.

Cỡ mẫu là: \(n = 21\).
Suy ra tứ phân vị thứ nhất \({Q_1}\)là \(\frac{{{x_5} + {x_6}}}{2}\). Do \({x_5};{x_6}\) đều thuộc nhóm [5;10) nên từ phân vị thứ nhất thuộc nhóm [5;10).
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{16}} + {x_{17}}}}{2}\) . Do \({x_{16}};\;{x_{17}}\)đều thuộc nhóm [10; 15) nên tứ phân vị thứ ba thuộc nhóm [10; 15).

Đáp án A
Số phần tử của không gian mẫu
*Gọi A là biến cố cần tính xác suất;
theo giả thiết bài toán chỉ có một cửa hàng mà có số khách vào là 3, 4 hoặc 5.
TH1: Một cửa hàng có 3 vị khách vào
+) Chọn 1 trong 5 cửa hàng có C 5 1 cách.
+) Chọn 3 trong 5 vị khách có C 5 3 cách.
+) 3 khách vừa chọn sẽ vào cửa hàng vừa chọn ở trên có 1 cách.
+) 2 khách còn lại mỗi khách có 4 lựa chọn nên có 4 2 cách.
Vậy trường hợp này có C 5 1 . C 5 3 . 4 2 cách.
TH2: Một cửa hàng có 4 vị khách vào, có tất cả C 5 1 . C 5 4 . 4 cách.
TH3: Một cửa hàng có 5 vị khách vào, có tất cả C 5 1 . C 5 5 cách.
![]()
Xác suất cần tính
![]()



Khách hàng nam ở khoảng tuổi \(\left[ {40;50} \right)\) mua bảo hiểm nhân thọ nhiều nhất.
Khách hàng nữ ở khoảng tuổi \(\left[ {30;40} \right)\) mua bảo hiểm nhân thọ nhiều nhất.
Ta có thể biết mốt của mẫu số liệu đó.