Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Định tính: khả năng bơi lội của học sinh(bơi thành thạo,biết bơi nhưng chưa thành thạo,chưa biết bơi)
Định lượng: Số lượng(250;175;75)
b:
Tổng số học sinh là:
250+175+75=500(bạn)
Số học sinh bơi thành thạo chiếm:
\(\dfrac{250}{500}=50\%\)
Số học sinh biết bơi nhưng chưa thành thạo chiếm:
\(\dfrac{175}{500}=35\%\)
Số học sinh chưa biết bơi chiếm:
100%-50%-35%=15%

a) Dữ liệu định tính: Khả năng biết bơi: chưa biết bơi; biết bơi; bơi giỏi.
Dữ liệu định lượng: Số bạn nam: 5; 8; 4
b) Dữ liệu chưa có tính đại diện cho khả năng bơi lội của các bạn học sinh lớp 7B vì còn thiếu dữ liệu về học sinh nữ của lớp

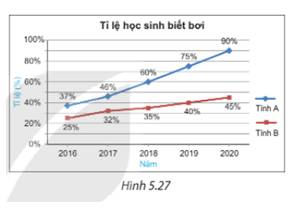
Tỉ lệ học sinh biết bơi của hai tỉnh A và B từ năm 2016 đến 2020 đều tăng.
Trong giai đoạn này, tỉnh A có tỉ lệ học sinh biết bơi tăng nhanh hơn vì độ dốc của biểu đồ đoạn thẳng của tỉnh A là lớn hơn.

16 lớp có số hs là:
35 x 16= 560(hs)
Các lớp còn lại có số hs là:
32 x (35-16)=608(hs)
Vậy có số hs là:
608+560=1168(hs)
Đáp số:1168 hs
16 lớp có số hs là:
35 x 16= 560(hs)
Các lớp còn lại có số hs là:
32 x (35-16)=608(hs)
Vậy có số hs là:
608+560=1168(hs)
Đáp số:1168 hs

Số lớp có 32 học sinh là :
35 - 16 =19 ( lớp )
Trường đó có tất cả số học sinh là :
16 x 35 + 19 x 32 = 1168 ( học sinh )
Đáp số : 1168 học sinh

Gọi số học sinh đăng kí ở lớp 7a,7b,7c lần lượt là a,b,c
Theo đề, ta có: a/9=b/8=c/7 và a+b+c=48
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{9}=\dfrac{b}{8}=\dfrac{c}{7}=\dfrac{a+b+c}{9+8+7}=\dfrac{48}{24}=2\)
=>a=18; b=16; c=14
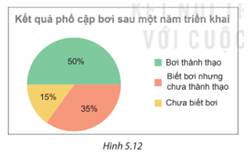

Số học sinh bơi thành thạo là: \(800.\frac{{50}}{{100}} = 400\)(học sinh)
Số học sinh chưa biết bơi là: \(800.\frac{{15}}{{100}} = 120\)(học sinh)