Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

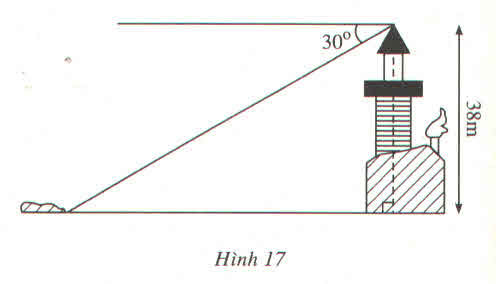
Khoảng cách từ đảo đến chân đèn là:
\(38\cdot\cot30^0\simeq65,818\left(cm\right)\)

Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28 ° , chiều cao tòa nhà là cạnh đối với góc nhọn.
Vậy chiếc ô tô đang đỗ cách tòa nhà:
60.cotg 28 ° ≈ 112,844 (m)

Phương pháp giải
Sử dụng: Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông kia nhân tan góc đối.

Đặt tên như hình vẽ thì chiều cao của tháp là đoạn BD
Xét tam giác ABC vuông tại A có AC=DE=150m;C^=200 nên
AB=150.tan20∘≈54,596(m)
Chiều cao của cột ăng-ten là:
BD=AB+AD

ta có : góc ACB= góc CAx= 28 độ ( so le trong)
- BC= AB x Cot 28 = 112 (m)
Vậy...

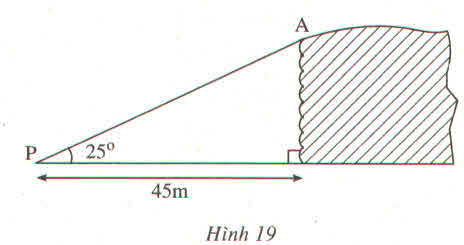
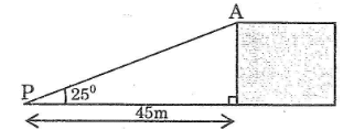
Chiều cao của vách đá là cạnh góc vuông đối diện với góc 25°
Khi đó chiều cao của vách đá là:
45.tg25 ≈ 20,984 (m)

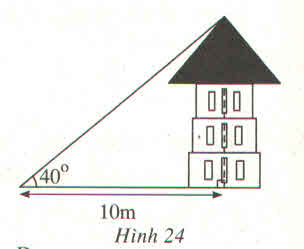
a. Chiều cao tòa nhà là cạnh góc vuông đối diện với góc 40o, khoảng cách từ chỗ người trinh sát đứng đến ngôi nhà là cạnh kề.
Chiều cao của tòa nhà là:
10.tg40o ≈ 8,391 (m)
b. Nếu dịch chuyển sao cho góc “nâng” là 35o thì anh ta cách tòa nhà:
8,391.cotg35o ≈ 11,934 (m)

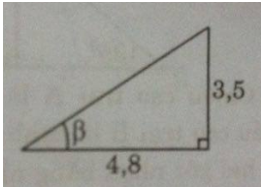
Chiều cao cột cờ là cạnh đối diên với góc giữa tia sang mặt trời và bóng cột cờ, chiều dài bóng là cạnh kề góc nhọn.
\(\tan B=\dfrac{35}{48}\)nên \(\widehat{B}=36^06'\)
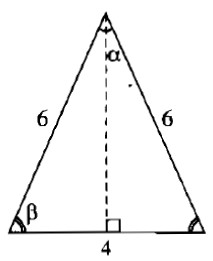
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.
Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.
Ta có: cosβ=26=13⇒β≈70∘32′cosβ=26=13⇒β≈70∘32′
Suy ra: α=180∘–(β+β)=180∘–2.70∘32'=38∘56′α=180∘–(β+β)=180∘–2.70∘32′=38∘56′
Vậy góc nhỏ nhất của tam giác bằng 38∘56′38∘56′.
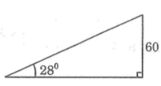
Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28°, chiều cao tòa nhà là cạnh đối với góc nhọn.
Vậy chiếc ô tô đang đỗ cách tòa nhà:
60.cotg28° ≈ 112,844 (m)