K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
V
1
15 tháng 11 2023
a: \(\dfrac{\sqrt{5}}{\sqrt{7}}=\dfrac{\sqrt{5\cdot7}}{7}=\dfrac{\sqrt{35}}{7}\)
b: \(\dfrac{2}{\sqrt{a}-1}=\dfrac{2\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}=\dfrac{2\sqrt{a}+2}{a-1}\)
H9
HT.Phong (9A5)
CTVHS
25 tháng 7 2023
\(\dfrac{4}{\sqrt{5}-\sqrt{2}}+\dfrac{3}{\sqrt{5}-2}-\dfrac{2}{\sqrt{3}-2}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{2}+\sqrt{5}\right)}+\dfrac{3\left(\sqrt{5}+2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}-\dfrac{2\left(\sqrt{3}+2\right)}{\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{5}\right)^2-\left(\sqrt{2}\right)^2}+\dfrac{3\left(\sqrt{5}+2\right)}{\left(\sqrt{5}\right)^2-2^2}-\dfrac{2\left(\sqrt{3}+2\right)}{\left(\sqrt{3}\right)^2-2^2}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{3}+\dfrac{3\left(\sqrt{5}+2\right)}{1}-\dfrac{2\left(\sqrt{3}+2\right)}{-1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{8\left(\sqrt{2}+\sqrt{5}\right)}{6}+\dfrac{18\left(\sqrt{5}+2\right)}{6}+\dfrac{12\left(\sqrt{3}+2\right)}{6}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{8\sqrt{2}+8\sqrt{5}+18\sqrt{5}+36+12\sqrt{3}+24-\sqrt{3}+1}{6}\)
\(=\dfrac{8\sqrt{2}+26\sqrt{5}+11\sqrt{3}+61}{6}\)
25 tháng 7 2023
\(=\dfrac{4\left(\sqrt{5}+\sqrt{2}\right)}{3}+\dfrac{3\left(\sqrt{5}+2\right)}{1}+\dfrac{2\left(2+\sqrt{3}\right)}{1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\sqrt{5}+4\sqrt{2}+9\sqrt{5}+18}{3}+\dfrac{4+2\sqrt{3}}{1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{2\left(13\sqrt{5}+4\sqrt{2}+18\right)+24+12\sqrt{3}-\sqrt{3}+1}{6}\)
\(=\dfrac{26\sqrt{5}+4\sqrt{2}+36+25+11\sqrt{3}}{6}\)
\(=\dfrac{61+11\sqrt{3}+26\sqrt{5}+4\sqrt{2}}{6}\)
18 tháng 12 2020
1) \(5\sqrt{8}-\dfrac{7}{2}\sqrt{72}+6\sqrt{\dfrac{1}{2}}\\ =5.\sqrt{4^2.\dfrac{1}{2}}-\dfrac{7}{2}.\sqrt{12^2.\dfrac{1}{2}}+6.\sqrt{\dfrac{1}{2}}=\left(5.4+\dfrac{7}{2}.12+6\right)\sqrt{\dfrac{1}{2}}\\ =68\sqrt{\dfrac{1}{2}}\)
2) \(\dfrac{6}{\sqrt{5}-1}=\dfrac{6.\left(\sqrt{5}+1\right)}{\left(\sqrt{5}-1\right).\left(\sqrt{5}+1\right)}=\dfrac{6\left(\sqrt{5}+1\right)}{5-1}\\ =\dfrac{6\left(\sqrt{5}+1\right)}{4}=\dfrac{3.\left(\sqrt{5+1}\right)}{2}\)
HQ
Hà Quang Minh
Giáo viên
20 tháng 7 2023
\(\sqrt{1+\dfrac{1}{ab}}=\sqrt{\dfrac{ab+1}{ab}}=\dfrac{\sqrt{ab\left(ab+1\right)}}{ab}=\dfrac{\sqrt{a^2b^2+ab}}{ab}\).
PT
1
22 tháng 7 2016
Ta có: \(\frac{1}{\sqrt[3]{9}-\sqrt[3]{6}+\sqrt[3]{4}}=\)\(\frac{\sqrt[3]{3}+\sqrt[3]{2}}{\left(\sqrt[3]{2}+\sqrt[3]{3}\right)\left(\sqrt[3]{9}-\sqrt[3]{6}+\sqrt[3]{4}\right)}=\frac{\sqrt[3]{2}+\sqrt[3]{3}}{\left(\sqrt[3]{2}\right)^3+\left(\sqrt[3]{3}\right)^3}=\frac{\sqrt[3]{2}+\sqrt[3]{3}}{5}\)
28 tháng 6 2016
\(\frac{\sqrt{6}}{3+\sqrt{2}-\sqrt{3}}=\frac{\sqrt{6}\left(3+\sqrt{2}+\sqrt{3}\right)}{\left(3+\sqrt{2}-\sqrt{3}\right)\left(3+\sqrt{2}+\sqrt{3}\right)}=\frac{3\sqrt{6}+2\sqrt{3}+3\sqrt{2}}{\left(3+\sqrt{2}\right)^2-3}\)
Ban tiep tuc khu mau roi lai su dung truc can thuc 1 lan nua la se co ket qua
PL
0
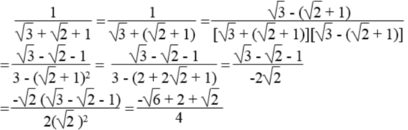
\(=\dfrac{3\sqrt{5}+3}{2}\)