Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Khoảng vân: i = 7 , 2 8 = 0 , 9 m m
Tại vị trí cách vân trung tâm 14,4mm = 16i có vân sáng bậc 16.

Chọn D
Trên bề rộng 7,2 mm của vùng giao thoa người ta đếm được 9 vân sáng (ở hai rìa là hai vân sáng) => 8i = 7,2mm => i = 0,9mm
Tại vị trí cách vân trung tâm 14,4 mm, ta được:
14,4mm = 16i
=> Vân sáng bậc 16

Đáp án C
+ 9 vân sáng ứng với 8 khoảng vân 8i = 7,2 mm → i = 0,9 mm.
+ Xét tỉ số: x i = 14 , 4 0 , 9 = 16 → vân sáng thứ 16

a. Bề rộng của 16 vân sáng là 15i, suy ra 15i=18mm --> i = 1,2 mm
Khoảng cách từ hai khe đến màn: \(D=\dfrac{ai}{\lambda}=\dfrac{1,2.1,2}{0,6}=2,4m\)
b. Bề rộng 21 vân sáng là 20 i', suy ra 20i' = 18mm ---> i'=0,9mm
Bước sóng: \(\lambda'=\dfrac{ai}{D}=\frac{1,2.0,9}{2,4}=0,45\mu m\)
c. Tại vị trí cách vân trung tâm x = 6mm
\(\Rightarrow x=6i=6,67i'\)
Nên tại vị trí này là vân sáng bậc 6 của bước sóng \(\lambda\)

Phương pháp:
Phương pháp: Vị trí vân sáng xs = ki
Cách giải: Đáp án C
Cách giải:
+ Khoảng cách giữa vân sáng bậc 2 và bậc 5 ở cùng một phía vân trung tâm là 3mm
=> 5i – 2i = 3mm => i = 1mm.
+ M ở trên vân trung tâm => xM = 0mm; xN = 1mm
+ Số vân sáng quan sát trên được trên vùng giao thoa MN bằng số giá trị k nguyên thoả mãn:
![]()
Có 12 giá trị của k thoả mãn => có 12 vân sáng.

Đáp án C
Phương pháp: Vị trí vân sáng xs = ki
Cách giải:
+ Khoảng cách giữa vân sáng bậc 2 và bậc 5 ở cùng một phía vân trung tâm là 3mm
=> 5i – 2i = 3mm => i = 1mm.
+ M ở trên vân trung tâm => xM = 0mm; xN = 1mm
+ Số vân sáng quan sát trên được trên vùng giao thoa MN bằng số giá trị k nguyên thoả mãn:
![]()
Có 12 giá trị của k thoả mãn => có 12 vân sáng.

Chọn C
Khoảng cách giữa vân sáng bậc 2 đến vân sáng bậc 5 ở cùng phía với nhau so với vân sáng trung tâm là 3 mm:
x = x5 - x2 = x2+3 - x3 = 3i
=> i = 1mm
Số vân sáng quan sát được trên vùng giao thoa đối xứng là:
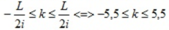
=> Có 11 giá trị của k thỏa mãn
Vậy trên màn có 11 vân sáng

Số vân sáng trong khoảng MN chính là số k thỏa mãn
\(x_M < x_s < x_N\)
=> \( 2 < k i < 4,5 \)
=> \(1,67 < k < 3,75.\)
Do \(k \in Z \) => \( k = 2,3.\)
Tương tự.
Số vân tối trong khoảng MN chính là số k thỏa mãn
\(x_M < x_t < x_N\)
=> \( 2 < (k+\frac{1}{2})i < 4,5\)
=> \( 1,167 < k < 3,25.\)
Do \(k \in Z \) => \(k = 2,3.\)
Vẫn chưa hiểu tại đoạn: k∈Z => k=2,3. Ai giải thích cho mình với ạ.
Đáp án C.
Khoảng vân: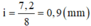
Tại vị trí cách vân trung tâm 14,4mm=16i có vân sáng bậc 16.