Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có i=1,1 mm.
L/2i = 7,7 =>
Trên màn có 15 vân sáng và 16 vân tối.

\(i = \frac{\lambda D}{a}= \frac{0,6.2,5}{1}=1,5 mm.\)
Số vân sáng quan sát trên màn
\(N_s = 2.[\frac{L}{2i}]+1=2.4+1 = 9.\)
Số vân tối quan sát trên màn
\(N_t = 2[\frac{L}{2i}+0,5]=2.4 = 8.\)
Tổng số vân sáng và vân tối là
\(N = N_t + N_s = 9+8 = 17.\)

Khoảng vân giao thoa :
![]()
Số khoảng vân trong một nửa bề rộng của miền giao thoa :
![]()
Số vân sáng trong một nửa bề rộng, không kể vân trung tâm là 4 vân. Số vân sáng trong cả bề rộng của miền giao thoa, kể cả vân trung tâm :
(2.4) + 1 = 9 vân
Số vân tối trong một nửa bề rộng : 4 vân.
Số vân tối trong cả bề rộng của miền giao thoa : 2. 4 = 8 vân.
Tổng số vân sáng và vân tối trong miền giao thoa : 9 + 8 = 17 vân.

Chọn B
Ta có:
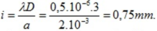
số vân sáng quan sát được trên vùng giao thoa đối xứng là:
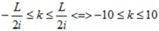
=> Có 21 giá trị của k thỏa mãn
Vậy trên màn hình có 21 vân sáng.
Số vân tối quan sát được trên vùng giao thoa đối xứng là:
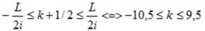
=> Có 20 giá trị k thỏa mãn
Vậy trên màn có 20 vân tối

Đáp án B.
Giữa hai điểm M và N có 10 vân tối và tại M và N đều là vân sáng. Như vậy trên MN, có tất cả 11 vân sáng và từ M đến N có khoảng 10 vân.




Cách giải: Đáp án A
Khoảng vân trong hệ giao thoa được xác định bởi biểu thức 6i = 3mm => i = 0,5 mm
Số vân tối trong cả trường giao thoa L = ki + b => 15 = 30.i + 0 => k = 30
Vậy có 30 vân tối trong hệ trường giao thoa