Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Khoảng cách nhỏ nhất bằng khoảng cách giữa hai vân sáng cùng bậc ∆ x = D λ 2 - λ 1 a = 0 , 4 mm.

Khoảng vân giao thoa :
![]()
Số khoảng vân trong một nửa bề rộng của miền giao thoa :
![]()
Số vân sáng trong một nửa bề rộng, không kể vân trung tâm là 4 vân. Số vân sáng trong cả bề rộng của miền giao thoa, kể cả vân trung tâm :
(2.4) + 1 = 9 vân
Số vân tối trong một nửa bề rộng : 4 vân.
Số vân tối trong cả bề rộng của miền giao thoa : 2. 4 = 8 vân.
Tổng số vân sáng và vân tối trong miền giao thoa : 9 + 8 = 17 vân.

- Khoảng vân của ánh sáng 1 là: 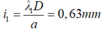
- Khoảng vân của ánh sáng 2 là: 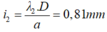
- Khi trên màn quan sát thấy vân tối thì đó là vân tối trùng nhau của hai ánh sáng 1 và 2. Xét tỉ số:
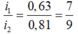
- Chuyển bài toán thành bài toán giao thoa với ánh sáng có bước sóng I’= 0,63.9 = 5,67mm
→ Trong miền L = 18mm có số vân tối là:
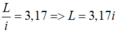
- Vậy nếu ở hai đầu là vân tối thì số vân tối nhiều nhất có thể là 4 vân.

Màu sắc của vân trung tâm được tạo thành do sự chồng chập của ba ánh sáng đơn sắc λ 1 , λ 2 , λ 3
Vậy toạ độ những vân sáng cùng màu vân trung tâm thoả mãn
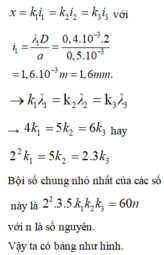

Vậy ta thấy giá trị khả dĩ lớn nhất của n bằng 4.
Vậy tổng số vân cùng màu vân trung tâm là N = 1 + 2.4 = 9 vân.
Đáp án C

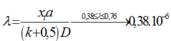
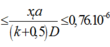
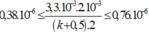



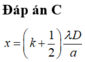
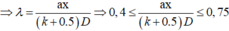
+ Khoảng vân \(i_1 = \frac{\lambda_1D}{a}=0,5\)mm, \(i_2=0,4\)mm.
+ Tìm khoảng cách gần nhất giữa 2 vân trùng, ta gọi là xT => xT = k1i1 = k2i2 => k1 λ1 = k2 λ2 =>\(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,4}{0,5}=\frac{4}{5}\) => k1= 4, k2 = 5.
=>\(x_T = 4.0,5=2\)mm.
+ Số vân của bước sóng 0,5 μm quan sát được: \(2.[\frac{13}{2.0,5}]+1=27\)
Số vân của bước sóng 0,4 μm quan sát được: \(2.[\frac{13}{2.0,4}]+1=33\)
Số vân trùng nhau quan sát đc: \(2.[\frac{13}{2.2}]+1=7\)
Vì mỗi vân trùng chỉ đc tính 1 lần nên tổng số vân quan sát đc là: 27 + 33 - 7 = 53.
Đáp án: A
A đó bạn