Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Từ (1); (2); (3) ta được tỷ lệ trên
Số vân sáng đơn sắc cần tìm là
![]() =16
=16

Đáp án B.
![]()
Vân sáng trùng màu với vân sáng trung tâm là những vân sáng thoả mãn:
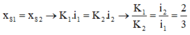
Vân sáng gần nhất cùng màu với vân sáng trung tâm ứng với:
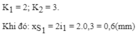

Đáp án B.
Ta có: x S 1 = K 1 . i 1 ; x S 2 = K 2 . i 2
Vân sáng trùng màu với vân sáng trung tâm là những vân sáng thoả mãn:
x S 1 = x S 2 → k 1 . i 1 = k 2 . i 2 → k 1 k 2 = i 2 i 1 = 2 3
Vân sáng gần nhất cùng màu với vân sáng trung tâm ứng với K 1 = 2 ; K 2 = 3 .
Khi đó: x S 1 = 2 i 1 = 2.0,3 = 0,6(mm)

Chọn D
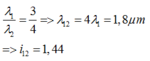
Trong khoảng đó (kể cả 2 đầu) có 5 vân của λ1, 4 vân của λ2, trừ đi 2 vân 2 đầu tính 2 lần => có 7 vân

- Điều kiện để hệ hai vân sáng trùng nhau:
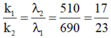
→ Giữa hai vân sáng cùng màu với vân trung tâm có 16 vân sáng của bức xạ λ2 và 22 vân sáng của bức xạ λ1.
→ Vậy có 38 vân sáng đơn sắc.

Đáp án B
+ Điều kiện để hệ hai vân sáng trùng nhau

→ Giữa hai vân sáng cùng màu với vân trung tâm có 16 vân sáng của bức xạ ![]() và 22 vân sáng của bức xạ
và 22 vân sáng của bức xạ ![]()
→ Vậy có 38 vân sáng đơn sắc.


Khi các vân sáng trùng nhau: \(k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)
k10,4 = k20,5 = k30,6 \(\Leftrightarrow\) 4k1 = 5k2 = 6k3
BSCNN(4,5,6) = 60
\(\Rightarrow\) k1 = 15 ; k2 = 12 ; k3 = 10 Bậc 15 của \(\lambda_1\) trùng bậc 12 của \(\lambda_2\) trùng với bậc 10 của \(\lambda_3\)
Trong khoảng giữa phải có: Tổng số VS tính toán = 14 + 11 + 9 = 34
Ta xẽ lập tỉ số cho tới khi k1 = 15 ; k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_2:\) \(\frac{k_1}{k_2}=\frac{\lambda_1}{\lambda_2}=\frac{5}{4}=\frac{10}{8}=\frac{15}{12}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k2 = 12 thì có tất cả 4 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 5 ; k2 = 4
Vị trí 3: k1 = 10 ; k2 = 8 => Trong khoảng giữa có 2 vị trí trùng nhau.
Vị trí 4: k1 = 15 ; k2 = 12
- Với cặp\(\lambda_2;\lambda_3:\) \(\frac{k_2}{k_3}=\frac{\lambda_3}{\lambda_2}=\frac{6}{5}=\frac{12}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k2 = 12 ; k3 = 10 thì có tất cả 3 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k2 = 6 ; k3 = 5 \(\Rightarrow\) Trong khoảng giữa có 1 vị trí trùng nhau.
Vị trí 3: k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_3:\) \(\frac{k_1}{k_3}=\frac{\lambda_3}{\lambda_1}=\frac{3}{2}=\frac{6}{4}=\frac{9}{6}=\frac{12}{8}=\frac{15}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k3 = 10 thì có tất cả 6 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 3 ; k3 = 2
Vị trí 3: k1 = 6 ; k3 = 4
Vị trí 4: k1 = 9 ; k3 = 6 \(\Rightarrow\) Trong khoảng giữa có 4 vị trí trùng nhau.
Vị trí 5: k1 = 12 ; k3 = 8
Vị trí 6: k1 = 15 ; k3 = 10
Vậy tất cả có 2 + 1 +4 = 7 vị trí trùng nhau của các bức xạ.
Số VS quan sát được = Tổng số VS tính toán – Số vị trí trùng nhau = 34 – 7 = 27 vân sáng.
\(\rightarrow D\)