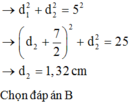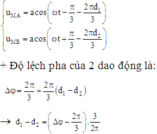Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Phương trình dao động của M đối với 2 nguồn là:
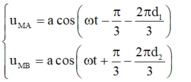
- Độ lệch pha của 2 dao động là:
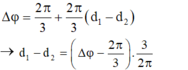
- M dao động với biên độ cực tiểu nên ta có:
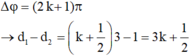
- Số điểm dao động với biên độ cực tiểu trên AB là:
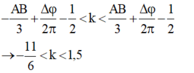
- Mà M cách B đoạn nhỏ nhất:
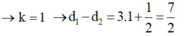
- Lại có:
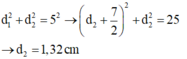

Đáp án C
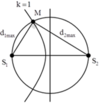
+ Điều kiện để một điểm M dao động cực đại và cùng pha với nguồn: d 2 - d 1 = k λ d 2 + d 1 = n λ
với k và n cùng chẵn hoặc cùng lẽ.
+ M gần trung trực nhất → k = 1 , để M nằm trong nửa đường tròn thì S 1 S 2 ≤ d 1 + d 2 ≤ d 1 m a x + d 2 m a x (1).
+ Với d 2 m a x - d 1 m a x = 4 d 2 m a x 2 + d 1 m a x 2 = 20 2 ⇒ d 1 m a x = 12 c m d 2 m a x = 16 c m
+ Thay vào (1), ta tìm được 5 ≤ n ≤ 7 , chọn 5, 7 (cùng lẻ vì k = 1), với n = 5 ứng với điểm nằm trên S 1 S 2 → trong đường tròn có 3 điểm cực đại, cùng pha với nguồn và nằm trên dãy k =1.

Đáp án B
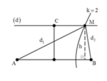
Ta có ![]() nên tam giác AMB vuông tại M.
nên tam giác AMB vuông tại M.
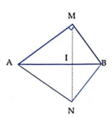
Mà ![]() suy ra IB= 9 cm.
suy ra IB= 9 cm.
Xét trên đoạn IM, số điểm dao động với biên độ cực đại là
![]() . Vậy trên đoạn IM có 1 điểm dao động với biên độ cực đại.
. Vậy trên đoạn IM có 1 điểm dao động với biên độ cực đại.
Do tính chất đối xứng IN cũng có một điểm dao động với biên độ cực đại.
Vậy trên MN có 2 điểm dao động vơi biên độ cực đại.

chọn đáp án D
Ta có
λ
=
2
c
m
M cách A, B các khoảng lần lượt là AM=19 cm, BM =21 cm là một vân cực đại bậc k với
A
M
-
B
M
=
k
λ
⇒
k
=
-
1
, hai nguồn đồng pha nên vân trung trực là vân cực đại bậc k=0
Vậy giữa M và đường trung trực của AB ko có vân cực đại nào nữa

Đáp án D
+ Số dãy cực đại trên đoạn
![]()
+ Để CM là lớn nhất thì M thuộc hypebol ứng với k=2
Ta có d 1 - d 2 = 8 cm
+ Với:
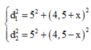
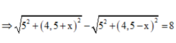
![]()