

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ACB) = α thì:
Khi b = 12 (cm), α = 42 ° thì
c = 12tg 42 ° ≈ 10,805 (cm), ∠ (ABC) = 48 ° , a = 12/(cos 42 ° ) ≈ 16,148 (cm).

Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ACB) = α thì:
AB = c = btg α , ∠ (ABC) = 90 ° - α , BC = a = b/cos α

Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ABC) = β thì:


Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan60^0=3\sqrt{3}\simeq5,1962\left(cm\right)\)
=>\(BC=\sqrt{AB^2+AC^2}=6\left(cm\right)\)

Trong tam giác ABC vuông tại A, cạnh AC = b, ∠ (ABC) = β thì:
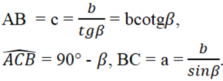

Bài 1:
a) Ta có:
\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)
\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)
b) Áp dụng Py-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+15^2=261\)
\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)
Bài 2:
\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)