Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

SABC = 3S
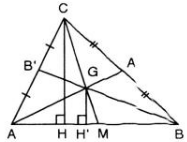
vì gọi M là trung điểm AB
kẻ CH \(\perp\) AB , GK \(\perp\) AB \(\Rightarrow\) CH // GK
G là trọng tâm \(\Delta\)ABC \(\Rightarrow\) GM = \(\frac{1}{3}\) CM \(\Rightarrow\) GK = \(\frac{1}{3}\) CH \(\Rightarrow\) Đpcm
Dựng GH, CK vuông góc với AB (H, K nằm trên AB)
Ta có GH // CK
G là trọng tâm của tgiác ABC (giao của hai trung tuyến), nên đừong trung tuyến thứ 3: CC' cũng đi qua G và: C'G / C'C = 1/3
Ta có:
GH / CK = C'G / C'C = 1/3
=> CK = 3GH
=> S(ABC) = (1/2)CK.AB = (1/2).(3)GH.AB = 3.S(ABG) = 3S

Vì G là trọng tâm tg ABC nên AG=2/3AA'
\(=>\frac{S_{ABG}}{S_{ABA'}}=\frac{2}{3}< =>S_{ABA'}=\frac{3}{2}S_{ABG}=\frac{3}{2}a\)
Ta có AA' là trung tuyến nên BC=2A'B
\(=>S_{ABC}=2S_{ABA'}=2.\frac{3}{2}a=3a\)
Vậy ...
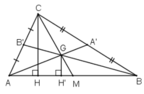
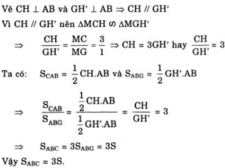
Vì \(CH\perp AB\)và \(GH'\perp AB\)=> CH // GH'
Vì \(CH//GH'\)nên \(\Delta MCH~\Delta MGH'\)
\(\Rightarrow\frac{CH}{GH'}=\frac{MC}{MG}=\frac{3}{1}=>CH=3GH'\)hay \(\frac{CH}{GH'}=3\)
Ta có : \(S_{CAB}=\frac{1}{2}CH.AB\)và \(S_{ABG}=\frac{1}{2}GH'.AB\)
\(\Rightarrow\frac{S_{CAB}}{S_{ABG}}=\frac{\frac{1}{2}CH.AB}{\frac{1}{2}GH'.AB}=\frac{CH}{GH'}=3\)
\(\Rightarrow S_{ABC}=3S_{ABG}=3S\)
Vậy : \(S_{ABC}=3S\)