Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
I nằm giữa O và A
=>OI+IA=OA
=>OI=OA-AI
=R-R'
=>(O) với (I) tiếp xúc nhau tại A
b: ΔIAD cân tại I
=>góc IAD=góc IDA
=>góc IDA=góc OAC
ΔOAC cân tại O
=>góc OAC=góc OCA
=>góc IDA=góc OCA
mà hai góc này đồng vị
nên ID//OC
c: Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó; ΔACB vuông tại C
Xét ΔACB vuông tại C có cos CAB=AC/AB=1/2*căn 3
=>góc CAB=30 độ
CB=căn AB^2-AC^2=R/2
\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{R\sqrt{3}}{2}\cdot\dfrac{1}{2}R=\dfrac{R^2\sqrt{3}}{8}\)
Xét ΔADO vuông tại D và ΔACB vuông tại C có
góc DAO chung
Do đó: ΔADO đồng dạng với ΔACB
=>\(\dfrac{S_{ADO}}{S_{ACB}}=\left(\dfrac{AO}{AB}\right)^2=\left(\dfrac{1}{4}\right)\)
=>\(S_{ODCB}=\dfrac{3}{4}\cdot S_{ACB}=\dfrac{3}{4}\cdot\dfrac{R^2\sqrt{3}}{8}=\dfrac{3\cdot\sqrt{3}\cdot R^2}{32}\)

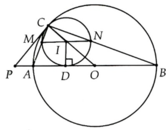
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm