Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có độ biến dạng của lò xo tại vị trí cân bằng: x = ∆ l = m g k = T 2 g 4 π 2 = 4 c m
Xét chuyển động của con lắc với thang máy: Chọn chiều dương hướng lên. Thang máy chuyển động nhanh dần đều ở vị trí: x = ∆ l .
Khi thang máy chuyển động, vị trí cân bằng bị dịch xuống dưới một đoạn bằng:
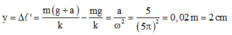
Nên li độ lúc sau là: x' = x + y.
Ta có:
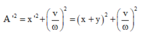
Từ đó ta có:
![]()
Thay số vào ta được:
![]()

Độ biến dạng của lò xo tại vị trí cân bằng: $x=\Delta l=\dfrac{mg}{k}=\dfrac{T^2 g}{4\pi ^2} = 4cm.$
Xét chuyển động của con lắc với thang máy: Chọn chiều dương hướng lên. Thang máy chuyển động nhanh dần đều ở vị trí $x=\Delta l.$
Khi thang máy chuyển động, vị trí cân bằng bị dịch xuống dưới một đoạn bằng: $y=\Delta l=\dfrac{m\left(g+a\right)}{k}-\dfrac{mg}{k}.$
Nên li độ lúc sau là: $x+y.$
Ta có: $A^2=x^2+\left(\dfrac{v}{\omega }\right)^2.$
$A^2=\left(x+y\right)^2+\left(\dfrac{v}{\omega }\right)^2.$
Từ đó ta có: $A^2=A^2+y^2+2xy.$
Tính ra: $A=3 \sqrt{5}.$

Đáp án D
+ Thang máy đứng yên: A = 50 − 32 2 = 9 ( c m ) Δ l = m g k = 16 ( c m )
+ Khi vật ở vị trí thấp nhất: x = A v à v = 0 .
+ Thang máy đi xuống nhanh dần đều => vật có gia tốc quán tính a hướng lên
⇒ g ' = g − a = 0 , 9 g ⇒ Δ l ' = m g ' k = 14 , 4 ( c m )
Lúc này vật có li độ x ' = A + ( Δ l − Δ l ' ) = 10 , 6 ( c m ) và vận tốc v = 0
Suy ra biên độ mới A ’ = 10 , 6 c m .

Đáp án D
Hướng dẫn:
Khi thang máy đứng yên, con lắc dao động điều hòa quanh vị trí cân bằng O, với biên độ A = l max − l min 2 = 48 − 32 2 = 8 cm.
+ Tại vị trí thấp nhất, thang máy chuyển động nhanh dần đều xuống dưới → con lắc chịu thêm tác dụng của lực quán tính hướng lên, làm vị trí cân bằng của vật lệc lên trên một đoạn O O ' = m a k = 0 , 4.0 , 1.10 25 = 1 , 6 cm.
→ Tại vị trí thang máy đi xuống, vật có x′ = 8 + 1,6 = 9,6 cm; v′ = 0.
→ Biên độ dao động mới của con lắc là A = 9,6 cm.

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Khi con lắc đơn qua VTCB thì thế năng bằng 0, động năng cực đại = cơ năng.
Thang máy đi lên nhanh dần thì vật vẫn đang ở vị trí thấp nhất nên thế năng = 0, trong khi đó, vận tốc không thay đổi --> Động năng không đổi = cơ năng ban đầu.
Do đó cơ năng lúc sau bằng động năng và bằng cơ năng ban đầu.
Gia tốc trọng trường lúc sau: g' < g nên biên độ giảm.

Khi lò xo bị giữ lại tại điểm chính giữa, nghĩa là chiều dài của lò xo chỉ còn một nửa như vậy độ cứng của lò xo tăng thêm 2 lần
Suy ra tần số góc của dao động mới \(\omega_2=\sqrt{\frac{2k}{m}}\) tăng lên \(\sqrt{2}\) so với tần số dao động cũ.
Khi qua vị trí cân bằng thì vận tốc cực đại được tình theo công thức
\(v_{max}=A\omega\)
Trong bài này vận tốc cực đại không đổi
\(A_2=\frac{A}{\sqrt{2}}\)

Đáp án D
Phương pháp: Sử dụng lí thuyết về bài toán thay đổi VTCB trong dao động điều hòa của CLLX thẳng đứng.
Cách giải:
Khi thang đứng yên, ở vị trí CB lò xo dãn một đoạn: ∆ l = m g k = 16 cm, biên độ dao động A = 8cm
Vật ở vị trí thấp nhất, lò xo dãn một đoạn: 16 + 8 = 24cm
Khi thang máy đi xuống nhanh dần đều với gia tốc a, vị trí CB mới là vị trí lò xo dãn một đoạn:


+ Khi vật đi qua vị trí cân bằng thi biên độ dao động của vật sẽ tăng lên.
Đáp án D