Bài 1.Vật có khối lượng m=200g được ném thẳng đứng từ dưới lên với vo =15m/s lấy g=10m/s :Hãy tính
a,Cơ năng lúc bắt đầu ném
b,Độ cao cực đại mà vật lên được
c,Độ cao mà vật tạo đó Wt=1/2 Wd
Bài 2.Một vật được ném thẳng đứng lên cao với vận tốc đầu v0 =6m/s.Bỏ qua sức cản không khí g=9,8m/s
a,Tính độ cao mà vật lên được
b,ở độ cao nào thế năng bằng động năng...
Đọc tiếp
Bài 1.Vật có khối lượng m=200g được ném thẳng đứng từ dưới lên với vo =15m/s lấy g=10m/s :Hãy tính
a,Cơ năng lúc bắt đầu ném
b,Độ cao cực đại mà vật lên được
c,Độ cao mà vật tạo đó Wt=1/2 Wd
Bài 2.Một vật được ném thẳng đứng lên cao với vận tốc đầu v0 =6m/s.Bỏ qua sức cản không khí g=9,8m/s
a,Tính độ cao mà vật lên được
b,ở độ cao nào thế năng bằng động năng ?Thế năng gấp 3 lần động năg
Bài 3 Vật m=3kg trượt không trên mặt ma sát không,vật tốc đầu từ đỉnh mặt phẳng nghiêng góc α=30 độ,dài L=10m.Lấy g=10m/s .Tính
a,Vận tốc ở chân mặt phẳng nghiêng
b,Khi đến vật ngang thì vật trượt được bao nhiêu mét mới dừng lại biết μ=0,1
c,Gỉa sử mặt phẳng nghiêng có ma sát μ=0,1.Tính vận tốc ở chân mặt nghiêng
Bài 4.Một người trượt batanh trên đoạn ngang BC không ma sát.Muốn vượt qua con dốc dài 4m nghiêng 30 độ dài tối thiểu phải là bao nhiêu?
Khối lượng người và xe là 60kg(g=10m/s)
a,Bỏ qua mọi ma sát trên dốc
b,ma sát trên dôc μ=0,2
c,Nếu vận tốc trên đoạn ngang là 10m/s thì người này trượt lên được tốc độ tối đa là bao nhiêu? Với ma sát trên dôc là μ=0,2 bỏ qua sức cản không khí
d,Tìm vận tốc trên BC để người trượt vượt qua dốc thì rơi xuống điểm E.Biết CE=10cm.Với ma sát trên dôc μ=0,2

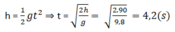

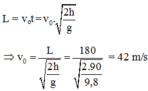
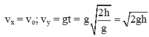
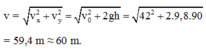

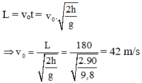
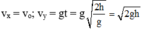
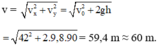

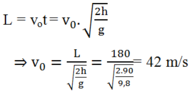
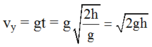
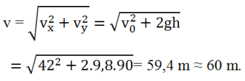


Đáp án B
Tầm bay xa của vận động viên là