Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Ta có ![]()
Do đó ![]()
Ta cũng có ![]() => n(A) = 8
=> n(A) = 8
Vậy xác suất của biến cố A là P(A) = 8 21

Đáp án A
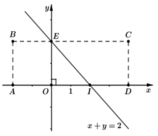
Để con châu chấu đáp xuống các điểm M(x; y) có x + y < 2 thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x; y) có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 , y ∈ { 0 ; 1 ; 2 }
Nếu x ∈ - 2 ; - 1 thì y ∈ { 0 ; 1 ; 2 } có 2.3 = 6 điểm
Nếu x = 0 thì y ∈ { 0 ; 1 } có 2 điểm
Nếu x =1 => y = 0 => có 1 điểm
=> có tất cả 6 + 2 + 1 = 9 điểm. Để con châu chấu nhảy trong hình chữ nhật mà đáp xuống các điểm có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 , y ∈ { 0 ; 1 ; 2 } . Số các điểm M(x; y) có tọa độ nguyên là: 7.3 = 21 điểm. Xác suất cần tìm là: P = 9 21 = 3 7 .

Chọn C
Lời giải. Số các điểm có tọa độ nguyên thuộc hình chữ nhật là 7.3 = 21 điểm vì
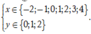
Để con châu chấu đáp xuống các điểm M(x,y) có x + y < 2
thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x,y) có tọa độ nguyên thì
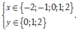
= Nếu x ∈ - 2 ; - 1 thì y ∈ 0 ; 1 ; 2
⇒ có 6 điểm
= Nếu x = 0 thì y ∈ 0 ; 1 ⇒ có 2 điểm
= Nếu x = 1 ⇒ y = 0 ⇒ có 1 điểm
⇒ có tất cả 6 + 2 +1 = 9 điểm thỏa mãn
Vậy xác suất cần tính P = 9 21 = 3 7

Chọn B
Số phần tử không gian mẫu ![]()
Gọi biến cố A = “Chọn 8 điểm sao cho không có 2 điểm nào có độ dài cung bằng 8 hoặc 3”.
Chia 24 điểm của đường tròn thành bảng sau:
| 1 |
9 |
17 |
| 4 |
12 |
20 |
| 7 |
15 |
23 |
| 10 |
18 |
2 |
| 13 |
21 |
5 |
| 16 |
24 |
8 |
| 19 |
3 |
11 |
| 22 |
6 |
14 |
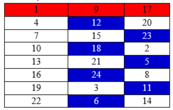
Trong đó, mỗi cột là tập các số có cùng số dư khi chia 3, mỗi hàng là tập các số có cùng số dư khi chia 8. Nhận thấy, mỗi cột không được chọn quá 4 số vì chọn từ 5 số trở lên, sẽ xuất hiện 2 số kề nhau tạo cung có độ dài là 3.
TH1: Chọn 4 số của cột 1 không kề nhau: 2 cách là {1;7;13;19} hoặc {4;10;16;22}
| 1 |
9 |
17 |
| 4 |
12 |
20 |
| 7 |
15 |
23 |
| 10 |
18 |
2 |
| 13 |
21 |
5 |
| 16 |
24 |
8 |
| 19 |
3 |
11 |
| 22 |
6 |
14 |
Tiếp theo, chọn 4 số a,b,c,d còn lại không nằm cùng hàng với 4 số của cột 1 và 2 số bất kỳ trong 4 số a,b,c,d cũng không được cùng hàng với nhau, có 2 4 cách chọn.
Vậy có 2. 2 4 = 32cách.
TH2: Chọn 3 số của cột 1 sao cho không có 2 số nào kề nhau: ![]()
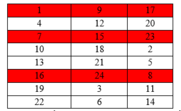
VD chọn{1;7;16} thì 5 số còn lai sẽ thuộc 3 nhóm màu trắng như hình vẽ. Khi đó mỗi nhóm màu trắng trong bảng chỉ có 2 cách chọn. Do đó TH2 có 16.2.2.2=128 cách.
TH3: Chọn 2 số không kề nhau của cột 1: C 8 2 - 8 = 20
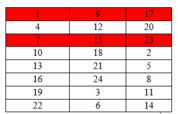
Khi đó, 6 hàng ngang còn lai chia làm 2 nhóm màu trắng như hình vẽ. Mỗi nhóm có đúng 2 cách chọn nên có 20.2.2 = 80 cách.
TH4: Chọn 1 số của cột 1 có 8 cách
TH5: Chỉ chọn cột 2 với 3. Ta có 2 cách chọn là các dòng xanh hoặc trắng: 2 cách.

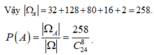

Chọn C
Mỗi bước người này có 2 lựa chọn sang trái hoặc phải nên số phần tử không gian mẫu là 2 10 .
Để sau đúng 10 bước người này quay lại đúng gốc tọa độ O thì người này phải sang trái 5 lần và sang phải 5 lần, do đó số cách bước trong 10 bước này là C 10 5 .
Xác suất cần tính bằng ![]() .
.
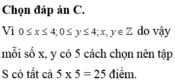


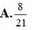
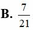



Đáp án A
Phương pháp:
+) Biểu diễn không gian mẫu dưới dạng tập hợp
tìm Ω
+) Gọi A là biến cố: “Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2”, biểu diễn A dưới dạng tập hợp và tìm số phần tử của A.
+) Tính xác suất của biến cố A: P(A) = A Ω
Cách giải:
Không gian mẫu
Có 9 cách chọn x, 9 cách chọn y, do đó Ω = 9.9 = 81
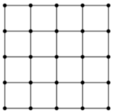
Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2 là hình tròn tâm O bán kính 2.
Gọi A là biến cố: “ Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2”