Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hoành độ giao điểm (P) ; (d) tm pt
\(\frac{1}{2}x^2-x-\frac{1}{2}m^2-m-1=0\)
\(\Leftrightarrow x^2-2x-m^2-2m-2=0\)
\(\Delta'=1-\left(-m^2-2m-2\right)=m^2+2m+3=\left(m+1\right)^2+2>0\)
Vậy pt luôn có 2 nghiệm pb
Theo Vi et \(\hept{\begin{cases}x_1+x_2=2\\x_1x_2=-m^2-2m-2\end{cases}}\)
Ta có \(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=68\)
\(\Leftrightarrow8-6\left(-m^2-2m-2\right)=68\)
\(\Leftrightarrow6m^2+12m-48=0\Leftrightarrow m=2;m=-4\)
Xét Pt hoành độ.......
\(\dfrac{1}{2}x^2=x+\dfrac{1}{2}m^2+m+1\\ \Leftrightarrow x^2-2x-m^2-2m-2=0\left(1\right)\)
Để ... thì Δ'>0
1+m2+2m+2>0 ⇔(m+1)2+2>0 (Hiển nhiên)
Với mọi m thì (1) sẽ có 2 nghiệm x1; x2.
*) Theo Hệ thức Viet ta có:
S=x1+x2=2 và P=x1x2= -m2-2m-2
*)Ta có:
\(\text{x^3_1 +x ^3_2 =68\Leftrightarrow(x_1+x_2)(x_1}^2-x_1x_2+x_2^2\left(\right)=68\\ \)
⇔(x1+x2)[(x1+x2)2-2x1x2-x1x2 ]=68 ⇔2[22-3(-m2-2m-2)]=68
⇔3m2+6m-24=0⇔m=2 và m=-4
KL:

a) Khi m = 2 thì: \(\hept{\begin{cases}y=x^2\\y=2x+3\end{cases}}\)
Hoành độ giao điểm (P) và (d) là nghiệm của PT: \(x^2=2x+3\Leftrightarrow x^2-2x-3=0\Leftrightarrow\left(x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\Rightarrow y=1\\x=3\Rightarrow y=9\end{cases}}\)
Vậy tọa độ giao điểm của (P) và (d) là \(\left(-1;1\right)\) và \(\left(3;9\right)\)
b) Hoành độ giao điểm của (P) và (d) là nghiệm của PT:
\(x^2=mx+3\Leftrightarrow x^2-mx-3=0\)
Vì \(ac=1\cdot\left(-3\right)< 0\) => PT luôn có 2 nghiệm phân biệt
Theo hệ thức viet ta có: \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=-3\end{cases}}\)
Mà \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{3}{2}\Leftrightarrow\frac{x_1+x_2}{x_1x_2}=\frac{3}{2}\Leftrightarrow\frac{-m}{3}=\frac{3}{2}\Rightarrow m=-\frac{9}{2}\)
Vậy \(m=-\frac{9}{2}\)

a) Xét phương trình hoành độ giao điểm chung của (d) và (P) :
\(x^2=\left(2m-1\right)x-m^2+2\)
\(\Leftrightarrow x^2-\left(2m-1\right)x+m^2-2=0\left(1\right)\)
Thay m=2 vào pt (1) ta được:
\(x^2-3x+2=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\Rightarrow y=1\\x=2\Rightarrow y=4\end{cases}}\)
Tọa độ giao điểm của (d) và (P) khi m=2 là \(A\left(1;1\right);B\left(2;4\right)\)
b) \(\Delta_{\left(1\right)}=\left(2m-1\right)^2-4m^2+8\)
\(=4m^2-4m+1-4m^2+8\)
\(=9-4m\)
Để pt (1) có 2 n ghiệm pb \(\Leftrightarrow9-4m>0\Leftrightarrow m< \frac{9}{4}\)
Theo hệ thức Vi-et ta có:
\(\hept{\begin{cases}x_1+x_2=2m-1\\x_1.x_2=m^2-2\left(1\right)\end{cases}}\)
Ta có: \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1-3x_2=7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3x_1+3x_2=6m-3\\x_1-3x_2=7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=\frac{3m+2}{2}\\x_2=\frac{m-4}{2}\end{cases}\left(3\right)}\)
Thay (3) vào (2) ta được:
\(\frac{3m+2}{2}.\frac{m-4}{2}=m^2-2\)
\(\Leftrightarrow\frac{3m^2-10m-8}{4}=m^2-2\)
\(\Rightarrow3m^2-10m-8=4m^2-8\)
\(\Leftrightarrow m^2+10m=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=0\\m=-10\end{cases}\left(tm\right)}\)
Vậy ...

- Phương trình hoành độ giao điểm của (P) và (d'):
\(-x^2=mx-4\Leftrightarrow x^2+mx-4=0\left(1\right)\)
\(a=1;b=m;c=-4\)
\(\Delta=b^2-4ac=m^2-4.\left(1\right).\left(-4\right)=m^2+16>0\)
Vì \(\Delta>0\) nên (P) và (d) luôn cắt nhau tại hai điểm phân biệt có hoành độ x1, x2.
Theo định lí Viete cho phương trình (1) ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{m}{1}=-m\\x_1x_2=\dfrac{c}{a}=\dfrac{-4}{1}=-4\end{matrix}\right.\)
Ta có: \(\left(x_1-x_2\right)^2-\left(x_1+x_2\right)=18\)
\(\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)=18\)
\(\Rightarrow\left(-m\right)^2-2.\left(-4\right)-\left(-m\right)-18=0\)
\(\Leftrightarrow m^2+m-12=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)
Vậy m=4 hay m=-3.

b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4
a: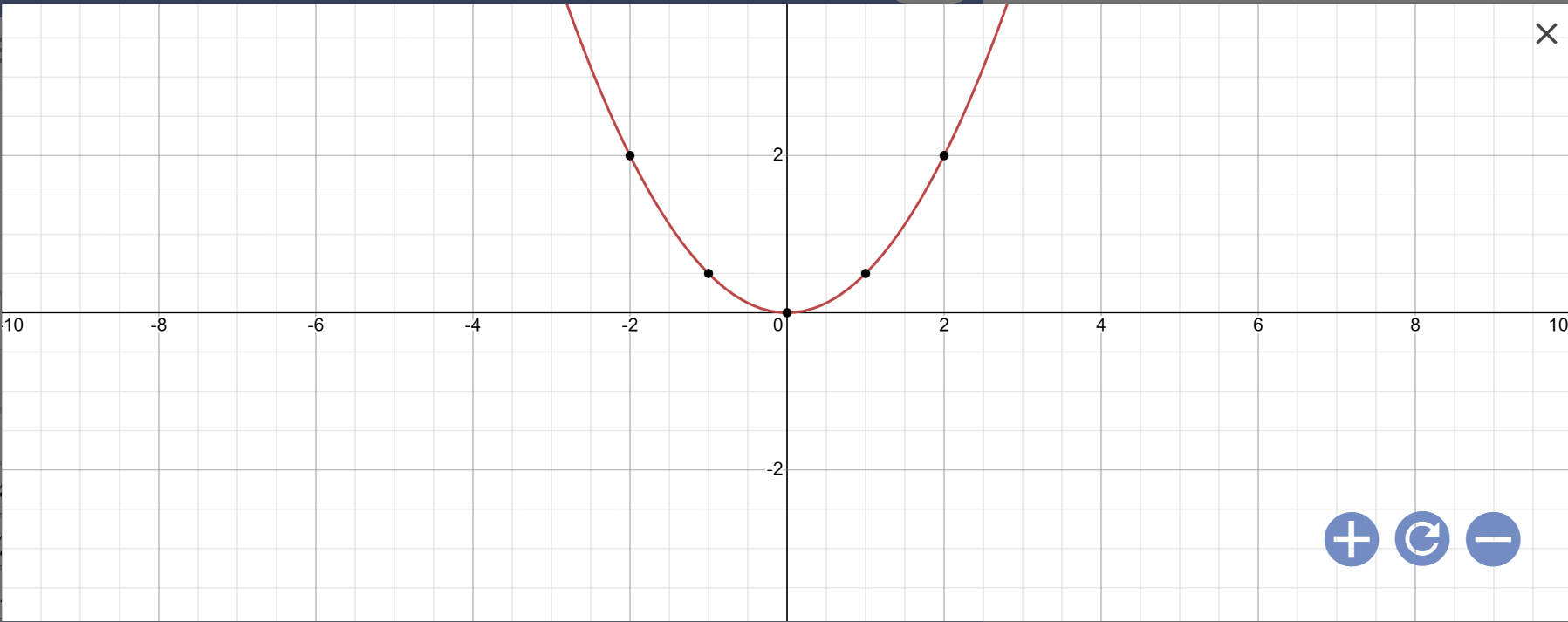
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=x+\dfrac{1}{2}m^2+m+1\)
=>\(x^2=2x+m^2+2m+2\)
=>\(x^2-2x-\left(m^2+2m+2\right)=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left[-\left(m^2+2m+2\right)\right]\)
\(=4+4\left(m^2+2m+2\right)\)
\(=4\left(m^2+2m+3\right)=4\left(m^2+2m+1+2\right)\)
\(=4\left(m+1\right)^2+8>=8>0\forall m\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=-\left(m^2+2m+2\right)\end{matrix}\right.\)
\(x_1^3+x_2^3=68\)
=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=68\)
=>\(2^3-3\cdot2\cdot\left[-\left(m^2+2m+2\right)\right]=68\)
=>\(6\left(m^2+2m+2\right)=60\)
=>\(m^2+2m+2=10\)
=>\(m^2+2m-8=0\)
=>(m+4)(m-2)=0
=>\(\left[{}\begin{matrix}m=-4\\m=2\end{matrix}\right.\)