Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
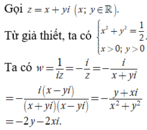
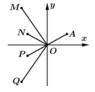
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (-2y;-2x) (đều có hoành độ và tung độ âm). Đồng thời 
Suy ra điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng 2OA. Quan sát hình vẽ ta thấy có điểm P thỏa mãn. Chọn D.
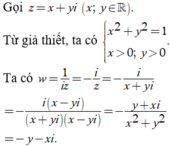
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (-y;-x) (đều có hoành độ và tung độ âm). Đồng thời 
Suy ra điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng OA. Quan sát hình vẽ ta thấy có điểm P thỏa mãn. Chọn C.
Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)
a. Số đoạn thẳng vẽ được là : \(C^2_{16}=120\)
b. Số tam giác tạo thành là : \(C^3_{16}=560\)
giải pt ta có
\(\begin{cases}z=2+\sqrt{5i}\\z=2-\sqrt{5}i\end{cases}\)
===> 2 điểm M,N lần lượt là M( 2, \(\sqrt{5}\)) VÀ N(2,-\(\sqrt{5}\))
MN=\(\sqrt{\left(2-2\right)^2+\left(-\sqrt{5}-\sqrt{5}\right)^2}\)=2\(\sqrt{5}\)
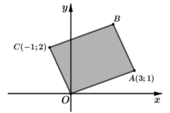
Vì OABC là hình bình hành nên
Suy ra số phức z 2 = 2 + 3 i có điểm biểu diễn là B.
Chọn B.
Gọi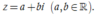
Suy ra điểm biểu diễn của z là điểm M(a;b)
Suy ra số phức 2z = 2a + 2bi có điểm biểu diễn trên mặt phẳng Oxy là M 1 (2a;2b)
Ta có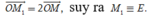
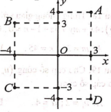
Chọn C.