Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Để (d) đi qua (0;-1) thì
Thay x=0 và y=-1 vào y=ax+b, ta được:
\(a\cdot0+b=-1\)
\(\Leftrightarrow b=-1\)
Vậy: (d): y=ax-1
Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=ax-1\)
\(\Leftrightarrow\dfrac{1}{2}x^2-ax+1=0\)
\(\Delta=a^2-4\cdot\dfrac{1}{2}\cdot1=a^2-2\)
Để (d) và (P) tiếp xúc với nhau thì \(\Delta=0\)
\(\Leftrightarrow a^2=2\)
hay \(a\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
Vậy: Để (d) tiếp xúc với (P) và (d) đi qua (0;-1) thì \(\left(a,b\right)=\left\{\left(\sqrt{2};-1\right);\left(-\sqrt{2};-1\right)\right\}\)

parabol (P): y = x 2 ; đường thẳng (d): y = 2x + m (m là tham số).
a) phương trình hoành độ giao điểm của (P) và (d) là:
x 2 = 2x + m ⇔ x 2 - 2x - m = 0
Δ'= 1 + m
(d) tiếp xúc với (P) khi phương trình hoành độ giao điểm có duy nhất 1 nghiệm
⇔ Δ'= 1 + m = 0 ⇔ m = -1
Khi đó hoành độ giao điểm là x = 1

Phương trình hoành độ giao điểm là:
\(x^2-2x-m^2-m+3=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(-m^2-m+3\right)\)
\(=4+4m^2+4m-12=4m^2+4m-8\)
\(=4\left(m+2\right)\left(m-1\right)\)
Để (P) tiếp xúc với (d) thì (m+2)(m-1)=0
=>m=-2(loại) hoặc m=1(nhận)

`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
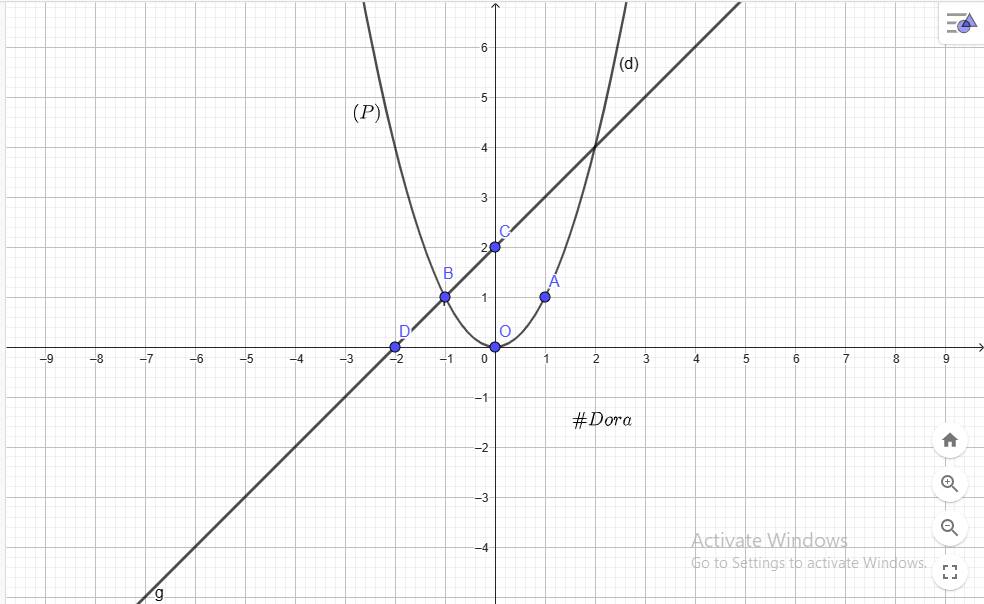
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`

a: Thay x=0 và y=9 vào (d), ta được:
\(b+6\cdot0=9\)
hay b=9
Vậy: (d): y=6x+9
b: Phương trình hoành độ giao điểm là:
\(ax^2-6x-9=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot a\cdot\left(-9\right)=36a+36\)
Để (d) tiếp xúc với (P) thì 36a+36=0
hay a=-1
`a)` Vì `(d)` đi qua `M(0;9)` nên thay `x=0` và `y=9` vào `(d)` có: `b=9`
`b)` Với `b=9=>(d):y=6x+9`
Xét ptr hoành độ của `(d)` và `(P)` có:
`ax^2=6x+9`
`<=>ax^2-6x-9=0` `(1)`
Để `(d)` tiếp xúc với `(P)` thì ptr `(1)` có nghiệm kép
`<=>\Delta' =0`
`<=>(-3)^2-a.(-9)=0`
`<=>a=-1` (t/m)

Đáp án B
Đường thẳng d và parabol (P) tiếp xúc với nhau khi phương trình a x 2 = m x + n ⇔ a x 2 - m x - n = 0 có nghiệm kép ( Δ = 0 )

b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4

ta có pt hoảnh độ giao điểm: \(ax^2=x-1\Leftrightarrow ax^2-x+1=0\)
P tiếp xúc d <=> PT trên có nghiệm kép <=> \(\Delta=0\Leftrightarrow1-4a=0\Leftrightarrow a=\frac{1}{4}\)