Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(C\right):x^2+y^2+4x-6y-12=0\)
\(\Leftrightarrow\left(C\right):\left(x+2\right)^2+\left(y-3\right)^2=25\)
\(\Rightarrow I=\left(-2;3\right)\) là tâm đường tròn, bán kính \(R=5\)
Kẻ IH vuông góc với AB.
\(\Rightarrow IH=\sqrt{R^2-AH^2}=\sqrt{5^2-\dfrac{1}{4}.50}=\dfrac{5\sqrt{2}}{2}\)
Đường thẳng AB có dạng: \(ax+by-2a=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;AB\right)=\dfrac{\left|-2a+3b-2a\right|}{\sqrt{a^2+b^2}}=\dfrac{5\sqrt{2}}{2}\)
\(\Leftrightarrow7a^2-48ab-7b^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=7b\\b=-7a\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}AB:7x+y-14=0\\AB:x-7y-2=0\end{matrix}\right.\)

Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
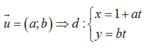
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
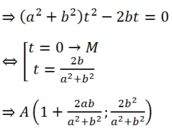
- Nếu d cắt (C2) tại B:
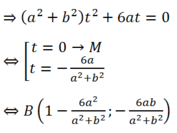
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
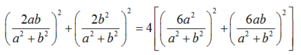
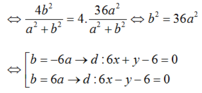
 ( hình như bài này còn cách khác nữa ...)
( hình như bài này còn cách khác nữa ...) 

Đường tròn (C) tâm \(I\left(1;1\right)\) bán kính \(R=4\)
\(\overrightarrow{IA}=\left(1;-1\right)\Rightarrow IA=\sqrt{2}\) (chà, rắc rối rồi, do \(\dfrac{IA}{R}< \dfrac{\sqrt{2}}{2}\) nên tam giác IMN không bao giờ có thể vuông được)
Ta có: \(S_{\Delta IMN}=\dfrac{1}{2}IM.IN.sin\widehat{MIN}=\dfrac{1}{2}R^2.sin\widehat{MIN}\)
\(\Rightarrow S_{IMN-max}\) khi \(sin\widehat{MIN}\) đạt max
Gọi H là trung điểm MN \(\Rightarrow IH\perp MN\Rightarrow IH\le IA\)
Do vai trò M, N là như nhau, không mất tính tổng quát, giả sử M, H nằm cùng phía so với A
\(cos\widehat{MIH}=\dfrac{IH}{IM}\le\dfrac{IA}{IM}=\dfrac{\sqrt{2}}{4}\Rightarrow\widehat{MIH}\ge69^018'\) (do \(0< \widehat{MIH}\le90^0\) nên \(cos\widehat{MIH}\) nghịch biến so với \(\widehat{MIH}\))
\(\Rightarrow\widehat{MIN}=2\widehat{MIH}>90^0\Rightarrow sin\widehat{MIN}\) nghịch biến so với \(\widehat{MIN}\)
\(\Rightarrow sin\widehat{MIN}_{max}\) khi \(\widehat{MIN}_{min}\)
Lại có: \(\widehat{MIN}=180^0-2.\widehat{IMH}\Rightarrow\widehat{MIN}_{min}\) khi \(\widehat{IMH}_{max}\)
\(\Rightarrow sin\widehat{IMH}_{max}\) (\(0\le\widehat{IMH}\le90^0\) nên \(sin\widehat{IMH}\) và \(\widehat{IMH}\) đồng biến)
\(sin\widehat{IMH}=\dfrac{IH}{IM}\le\dfrac{IA}{IM}\Rightarrow sin\widehat{IMH}_{max}\) khi H trùng A
Hay \(S_{\Delta IMN-max}\) khi H trùng A \(\Leftrightarrow d\perp IA\)
\(\Rightarrow d\) nhận (1;-1) là 1 vtpt
Phương trình d: \(1\left(x-2\right)-y=0\Leftrightarrow x-y-2=0\)