Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

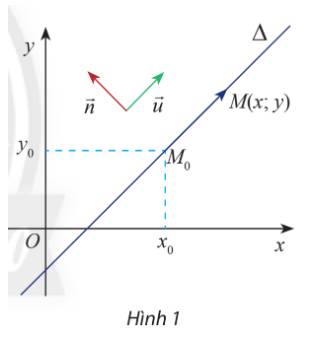
\(\Delta \) nhận vectơ \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến, suy ra vectơ chỉ phương của \(\Delta \) là \(\overrightarrow u = (b; - a)\)
M và \({M_0}\) thuộc đường thẳng \(\Delta \) nên \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\), suy ra \(\left\{ \begin{array}{l}{x_0} - x = b\\{y_0} - y = - a\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - b\\y = {y_0} + a\end{array} \right.\)
Suy ra \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
Thay tọa độ điểm M vào phương trình \(ax + by + c = 0\) ta có:
\(a\left( {{x_0} - b} \right) + b\left( {{y_0} + a} \right) + c = \left( { - ab + ba} \right) + \left( {a{x_0} + b{y_0} + c} \right) = 0\) (đúng vì \( - a{x_0} - b{y_0} = c\))
Vậy \(M(x;y)\) thỏa mãn phương trình đã cho

a) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)

a) Biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \) là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\)
b) Ta có:
\(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = \left( {x - {x_0}} \right)\left( {a - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right)\)
c) \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0 \Rightarrow \overrightarrow {{M_0}M} \bot \overrightarrow {{M_0}I} \)
Mà \({M_0}I\) là đoạn thẳng nối tâm với điểm nằm ngoài
Vậy ta thấy pt đường thẳng \(M{M_0}\) là tiếp tuyến của đường tròn tại điểm \({M_0}\)

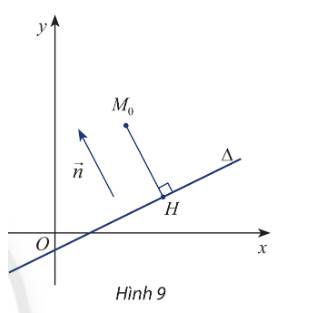
a) Ta có: \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Mà H là hình chiếu vuông góc của \({M_0}\) trên \(\Delta \) nên \(H{M_0} \bot \Delta \)
Mặt khác vectơ pháp tuyến \(\overrightarrow n \) cùng vuông góc với \(\Delta \)
Suy ra \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương (đpcm)
b) Ta có: \(\overrightarrow n = (a;b)\) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Suy ra \(p = \overrightarrow n .\overrightarrow {H{M_0}} = a\left( {{x_0} - {x_H}} \right) + b\left( {{y_0} - {y_H}} \right) = a{x_0} + b{y_0} - \left( {a{x_H} + b{y_H}} \right)\) (1)
Mà H thuộc đường thẳng \(\Delta \) nên tọa độ điểm H thỏa mãn phương trình đường thẳng \(\Delta \)
Thay tọa độ điểm H vào phương trình \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) ta có:
\(a{x_H} + b{y_H} + c = 0 \Leftrightarrow c = - \left( {a{x_H} + b{y_H}} \right)\)
Thay \(c = - \left( {a{x_H} + b{y_H}} \right)\) vào (1) ta có
\(p = a{x_0} + b{y_0} + c\) (đpcm)
c) Ta có: \(p = \overrightarrow n .\overrightarrow {H{M_0}} \Leftrightarrow \overrightarrow {H{M_0}} = \frac{p}{{\overrightarrow n }} \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \left| {\frac{p}{{\overrightarrow n }}} \right| \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)

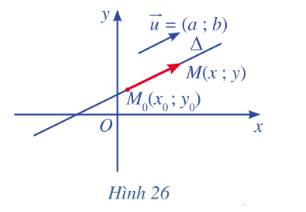
a) Hai vectơ \(\overrightarrow u {\rm{ }}\)và \(\overrightarrow {{M_o}M} \)cùng phương với nhau.
b) Xét \(M\left( {x;y} \right)\). Vì cùng phương với nên có số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }}\)
c) Do \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\) nên:
\(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x - {x_o} = at\\y - {y_o} = bt\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {x_o} + at\\y = {y_o} + bt\end{array} \right.\)
Vậy tọa độ điểm M là: \(M\left( {{x_o} + at;{y_o} + bt} \right)\)

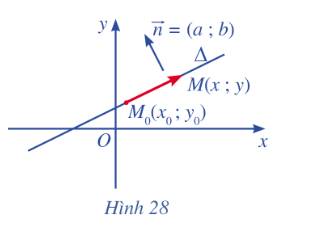
Gọi \(M\left( {x;y} \right)\)
Ta có: \(\overrightarrow {AM} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow n = \left( {a;b} \right)\)
\( M \in \Delta \Leftrightarrow \overrightarrow {AM} \bot \overrightarrow n \)
Hay \(\overrightarrow {AM} .\overrightarrow n = 0 \Leftrightarrow a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0\) (ĐPCM).

a) Vì \(\overrightarrow {OA} = \overrightarrow u = (x;y)\) nên A(x; y).
Tương tự: do \(\overrightarrow {OB} = \overrightarrow v = \left( {x';y'} \right)\) nên B (x’; y’)
b) Ta có: \(\overrightarrow {OA} = (x;y) \Rightarrow O{A^2} = {\left| {\overrightarrow {OA} } \right|^2} = {x^2} + {y^2}.\)
Và \(\overrightarrow {OB} = (x';y') \Rightarrow O{B^2} = {\left| {\overrightarrow {OB} } \right|^2} = x{'^2} + y{'^2}.\)
Lại có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
\( \Rightarrow A{B^2} = {\left| {\overrightarrow {AB} } \right|^2} = {\left( {x' - x} \right)^2} + {\left( {y' - y} \right)^2}.\)
c) Theo định lí cosin trong tam giác OAB ta có:
\(\cos \widehat O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Mà \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = OA.OB.\cos \widehat O\)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = OA.OB.\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{2}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{{x^2} + {y^2} + x{'^2} + y{'^2} - {{\left( {x' - x} \right)}^2} - {{\left( {y' - y} \right)}^2}}}{2}\\ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{ - \left( { - 2x'.x} \right) - \left( { - 2y'.y} \right)}}{2} = x'.x + y'.y\end{array}\)

a) Phương của hai vecto \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau.
b) Ta có: \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\)
Xét điểm \(M\left( {x;y} \right) \in \Delta \). Vì \(\overrightarrow {{M_o}M} \bot \overrightarrow n \) nên: \(\overrightarrow {{M_o}M} .\overrightarrow n = 0 \Leftrightarrow a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0 \Leftrightarrow ax + by - a{x_o} + b{y_o} = 0\)

Ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}.\)
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\) mà \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương nên ta có:
\(\left\{ \begin{array}{l}{x_0} - x = {u_1}\\{y_0} - y = {u_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - {u_1}\\y = {y_0} - {u_2}\end{array} \right.\)
Vậy \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)