Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

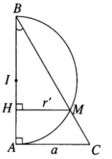
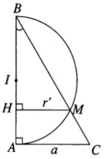
Khi quay xung quanh trục AB, giao điểm M của nửa đường tròn đường kính AB và cạnh CD sẽ tọ nên giao tuyến của mặt nón và mặt cầu.
Vẽ MH ⊥ AB
Ta có:
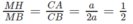
Mặt khác ta có CA 2 = CM.CB nên ta có
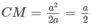
Do đó: BM = CB − CM = 3a/2 và HM = 3a/4

Gọi S 1 là diện tích toàn phần của hình nón và S 2 là diện tích mặt cầu.
Ta có: S 1 = πrl + πr 2 = 3 πa 2
S 2 = 4 πr 2 = 3 πa 2
Vậy S 1 = S 2

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)

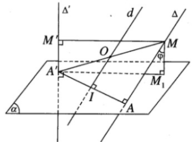
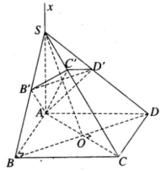
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

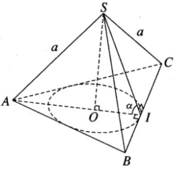
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 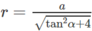
Hình nón nội tiếp có đường sinh là :
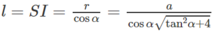
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()
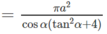


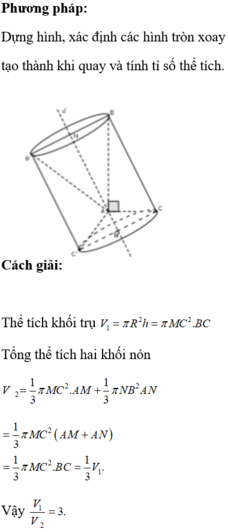


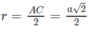
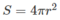
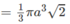
Tam giác vuông ABC có BC = 2a và AC = a nên ta suy ra ∠ ABC = 30 ° . Khi quay xung quanh trục AB cạnh BC tạo nên mặt nón tròn xoay có góc ở đỉnh bằng 60 ° và có đường tròn đáy có bán kính AC = a. Khi xoay xung quanh trục AB nửa đường tròn đường kính AB tạo nên mặt cầu có tâm là trung điểm I để đoạn AB và bán kính r = AB/2.