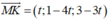Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương trình tham số của đường thẳng d qua điểm M(-2;3;1) và có vectơ chỉ phương
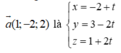

Chọn C
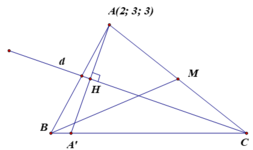
Gọi M là trung điểm của AC. Khi đó M thuộc vào đường trung tuyến kẻ từ B của tam giác ABC.
Giả sử M (3 – t ; 3 + 2t ; 2 – t) ∈ Δ suy ra C (4-2t; 3+4t; 1-2t).
Mà C thuộc và đường phân giác trong d của góc C nên ta có: 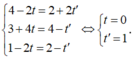
Suy ra C (4; 3; 1).
Gọi H là hình chiếu vuông góc của A trên đường phân giác trong d.
Suy ra H (2+2t';4-t';2-t') ![]()
Ta có ![]() ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
=> H (2;4;2).
Gọi A' đối xứng với A qua đường phân giác trong d.
Suy ra A’ ∈ (BC) và A' (2;5;1). Khi đó ![]() là vectơ chỉ phương của đường thẳng BC.
là vectơ chỉ phương của đường thẳng BC.

Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương ![]()

Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương ![]()

Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương u → 2 ; - 1 ; 3 .





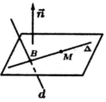
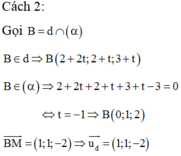
Chọn B
Phương trình tham số của đường phân giác trong góc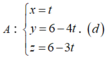
Gọi D là điểm đối xứng với M qua (d). Khi đó D ∈ AC => đường thẳng AC có một vectơ chỉ phương là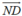 .
.
Ta xác định điểm D.
Gọi K là giao điểm MD với (d). Ta có K (t;6-4t;6-3t);