

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Phương pháp giải: Áp dụng công thức tính khoảng cách từ điểm đến mặt phẳng.
Khoảng cách từ điểm M ( x 0 ; y 0 ; z 0 ) đến mặt phẳng (P): Ax+By+Cz+D = 0 là:
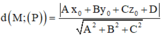
Lời giải:
Khoảng cách từ điểm M đến mặt phẳng (P) là: 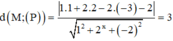

Đáp án A
Khoảng cách từ điểm M đến mặt phẳng (P) là:
d M ; P = 2.1 − 2 − 2 − 13 + 3 2 2 + − 2 2 + − 1 2 = 4 3

Đáp án D
Phương pháp:
+ Tìm tâm và bán kính của mặt cầu
+ Xác định vị trí tương đối của mặt phẳng và mặt cầu để suy ra vị trí của điểm M
+ Tìm tọa độ của đường thẳng và mặt cầu thì ta giải hệ phương trình gồm phương trình đường thẳng và phương trình mặt cầu
Cách giải:
Mặt cầu (S) có tâm
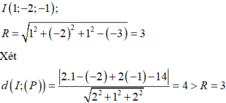
nên mặt phẳng (P) không cắt mặt cầu (S).Khi đó điểm M thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là nhỏ nhất thì M là giao điểm của đường thẳng d đi qua I , nhận n P → = 2 ; - 1 ; 2 làm VTCP với mặt cầu.
Phương trình đường thẳng
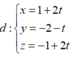
Tọa độ giao điểm của đường thẳng d và mặt cầu (S) thỏa mãn hệ phương trình
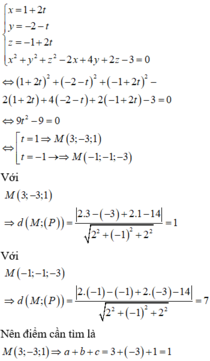

Chọn A.
Phương pháp: Điểm M là một trong hai giao điểm của đường thẳng (đi qua tâm mặt cầu và vuông góc với mặt phẳng) với mặt cầu.
Cách giải: Phương trình đường thẳng d đi qua tâm mặt cầu vuông góc với mặt phẳng (P) là:

Vậy M = (-1;-1;-3)