Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Giả sử mặt cầu (S) có tâm I a ; 0 ; 0 ∈ O x , bán kính R > 0 . Khi đó phương trình mặt cầu (S) là x − a 2 + y 2 + z 2 = R 2 .
Gọi H,K lần lượt là hình chiếu của I trên (P) và (Q) , khi đó:
I H = d I ; P = a + 1 6 và I K = d I ; Q = 2 a − 1 6
Do I H 2 + 4 = R 2 và I K 2 + r 2 = R 2 nên a + 1 2 6 + 4 = R 2 2 a − 1 2 6 + r 2 = R 2
⇒ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a + 1 2 + 24 = 2 a − 1 2 + 6 r 2
⇔ a 2 − 2 a + 2 r 2 − 8 = 0 *
Để có duy nhất một mặt cầu (S) thì phương trình (*) phải có một nghiệm
⇔ Δ ' = 1 − 2 r 2 − 8 = 0 ⇔ r 2 = 9 2 . Do r > 0 nên r = 3 2 .

Đáp án A
Phương pháp:
+) Viết phương trình mặt phẳng (ABC) ở dạng đoạn chắn, thay tọa độ điểm M vào pt mặt phẳng (ABC).
+) (ABC) tiếp xúc với mặt cầu (S) tâm I bán kính R ó d(I;(ABC)) = R
Cách giải:
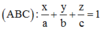
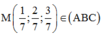
![]()
(ABC) tiếp xúc với mặt cầu (S) có tâm I(1;2;3) và bán kính R = 72 7
![]()
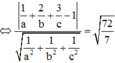
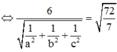
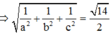


Chọn đáp án A
Ta có C = S 1 ∩ S 2
⇒ Mặt phẳng (P) chứa đường tròn (C) có phương trình thỏa mãn
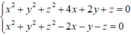
![]()
Phương trình mặt phẳng (ABC) là:
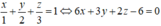
Suy ra (P) // (Q)
Mặt cầu (S) tiếp xúc với ba đường thẳng AB, BC, CA sẽ giao với mặt phẳng (ABC) theo một đường tròn tiếp xúc với ba đường thẳng AB, BC, CA.
Trên mặt phẳng (ABC) có 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA; đó là đường tròn nội tiếp tam giác ABC và ba đường tròn bàng tiếp các góc A, B, C. Do đó có 4 mặt cầu, tâm nằm trên mặt phẳng (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA
Tâm của 4 mặt cầu này là hình chiếu của tâm 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA lên mặt phẳng (P).


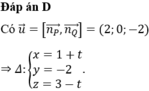



Đáp án A
Ba điểm A,B,C tạo thành một tam giác. Có 4 đường tròn tiếp xúc với cả ba đường thẳng AB,AC,BC (hình vẽ trên).
Mặt cầu (S) cần tìm tiếp xúc với 3 đường thẳng AB,AC,BC, do đó nó phải chứa 1 trong 4 đường tròn trên.
Xét với 1 đường tròn bất kì trong 4 đường tròn trên, giả sử là đường tròn tâm (O) nằm bên trong tam giác, ta có:
Tâm I của mặt cầu (S) phải nằm trên đường thẳng d đi qua tâm O và vuông góc với (ABC). Mặt khác, I thuộc mp (P) chứa (C), (C) lại không vuông góc với (ABC) do đó chỉ có 1 giao điểm của d với (P). Tương tự, với 3 đường tròn còn lại, với mỗi đường tròn ta tìm được 1 tâm I nữa. Vậy có 4 mặt cầu thỏa mãn yêu cầu.