Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng d đi qua A ( 1;-1;2 ) có vec tơ chỉ phương u → ( a ; b ; c ) do d song song (P): 2x - y - z + 3 = 0 nên u → ( a ; b ; c ) ⊥ n ( 2;-1;1 )
⇔ u → . n = 0 ⇔ 2a = b + c
Đến đây ta kiểm tra chỉ có đáp án A là đường thẳng có véc tơ chỉ phương thỏa mãn (1) nên ta chọn đáp án A
Đáp án cần chọn là A

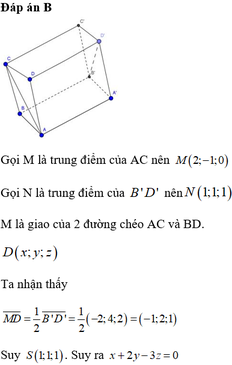
Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8

Đáp án A.
Ta có: u d . n p = - 2 - 2 + 4 = 0 nên [ d / / ( P ) d ⊂ P
Mặt khác điểm A(1;0;3) và A(1;0;3) ∈ P nên d nằm trên (P).



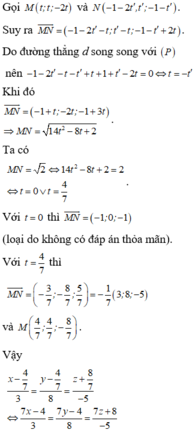
Đáp án A.
Ta có u 1 = 2 ; - 1 ; 1 và u 2 = - 2 ; 1 ; - 1 suy ra u 1 → = - u 2 → .
Mặt khác M ( 3 ; 1 ; 2 ) ∈ d 1 và M ∈ d 2 suy ra d 1 và d 2 trùng nhau.