Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
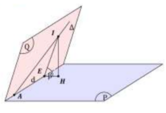

Khi đó đường thẳng d vuông góc với ∆ tại A. Chọn u d → = u Δ → , n P → = − 1 ; 6 ; 4 .
Như vậy (Q) là mặt phẳng chứa hai đường thẳng cắt nhau a và ∆ .
Do đó (Q) đi qua A và nhận vectơ u Q → = u Δ → , u d → = 10 ; − 7 ; 13 .
Phương trình mặt phẳng Q : 10 x − 2 − 7 y − 1 + 13 z = 0 ⇔ 10 x − 7 y + 13 z − 13 = 0
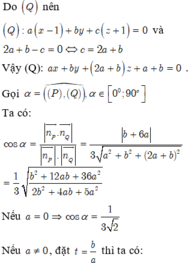
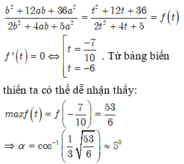


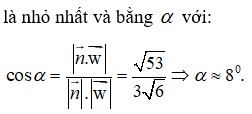

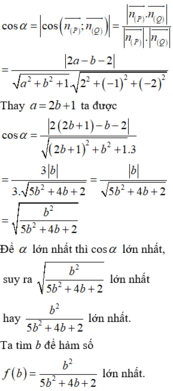

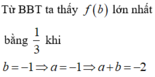

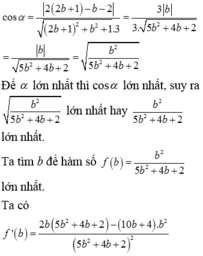
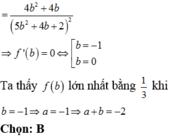



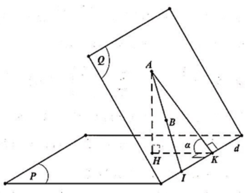
Gọi n ( a,b,c ) là VTPT của (Q)
⇒ n a , b , c . u 2 ; 1 ; - 1 = 0 ⇔ 2 a + b - c = 0 ⇒ c = 2 a + b
Khi đó góc α giữa hai mặt phẳng (P) và (Q) nhỏ nhất khi lớn nhất với
là VTPT của ta có
cos α = n . n ' → n → . n ' → = 2 z - b + 2 c 3 a 2 + b 2 + c 2 = 6 a + b 3 5 a 2 + 4 a b + 2 b 2
⇒ P 2 = 36 a 2 + 12 a b + b 2 9 5 a 2 + 4 a + 2 b 2 = 36 t 2 + 12 t + 1 9 5 a 2 + 4 a + 2 b 2
Xét hàm số
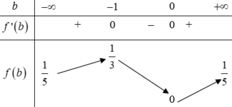
f t = 36 t 2 + 12 t + 1 9 5 a 2 + 4 a + 2 b 2 ⇒ f ' t = 2 42 t 2 + 67 t + 10 9 5 a 2 + 4 a + 2 b 2 = 0 ⇔ t = - 1 6 t = - 10 7
Vậy GTLN của P = f - 10 7 = 53 54 = 0 , 99
⇒ α = 8 o
Đáp án cần chọn là B