Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
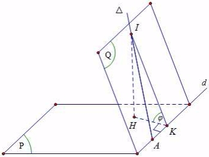Gọi
A
=
∆
∩
P
;
d
=
P
∩
Q
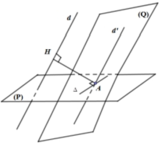
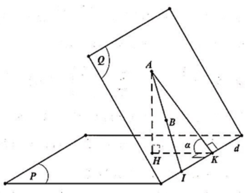
Lấy I ∈ ∆ ⇒ A ; I cố định, kẻ I H ⊥ P ; H K ⊥ d ⇒ P ; Q ^ = I K H ^ = φ
Do I A ≥ I K ⇒ sin φ = I H I K ≥ I H I A ⇒ φ m i n khi K ≡ A tức là I A ⊥ d ⇒ n Q → = u ∆ → ; u d →
Trong đó n ∆ ¯ = 1 ; - 2 ; - 2 ; u d ¯ = u ∆ ¯ ; u P ¯ = 3 ; 0 ; 3 = 3 1 ; 0 ; 1
Suy ra n Q ¯ = u ∆ ¯ ; u d ¯ = - 2 1 ; 1 ; - 1 , mặt khác (Q) chứa đường thẳng ∆ nên (Q) đi qua điểm (1;2;-1)
Do đó Q : x + y - z - 4 = 0 ⇒ A 4 ; 0 ; 0 , B ( 0 ; 4 ; 0 ) , C ( 0 ; 0 ; - 4 ) ⇒ V O . A B C = 64 6 = 32 3
Kiểm tra ta thấy d cắt (P)
Đường thẳng cần tìm là giao tuyến của mặt phẳng α với mặt phẳng (P)
Trong đó mặt phẳng α đi qua điểm A và vuông góc với đường thẳng AH, điểm H là hình chiếu của A trên đường thẳng d
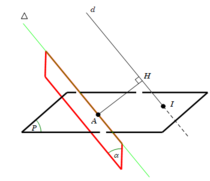
Ta tìm được tọa độ điểm H(-1;0;2) => phương trình mp
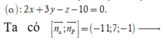đường thẳng
∆
có một VTVP là
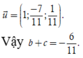
Chọn A.
Đáp án A
Phương pháp:
Đánh giá, tìm vị trí của Δ để khoảng cách giữa 2 đường thẳng là lớn nhất.
Cách giải:
Kẻ AH vuông góc d, qua A kẻ d ' / / d .
Dựng mặt phẳng (Q) chứa d’ và vuông góc AH, (Q) cắt (P) tại Δ 0 . Ta sẽ chứng minh Δ 0 thỏa mãn yêu cầu đề bài (cách d một khoảng cách lớn nhất).
Vì A H ⊥ d A H ⊥ Q ⇒ d / / Q ⇒ d d ; Q = A H = d d ; Δ 0
(do Δ 0 ⊂ Q )
Lấy Δ là đường thẳng bất kì qua A và nằm trong (P). Gọi (Q’) là mặt phẳng chứa d’ và
Δ ⇒ d / / Q '
⇒ d d ; Q ' = d H ; Q '
Kẻ
H A ' ⊥ Q ' , A ' ∈ Q ' ⇒ d d ; Q ' = H A ' = d d ; Δ .
Ta có: H A ' ≤ H A ⇒ Khoảng cách từng d đến Δ lớn nhất bằng AH khi Δ trùng Δ 0.
*) Tìm tọa độ điểm H:
Gọi α : mặt phẳng qua A vuông góc d
⇒ α : 2. x − 1 − 1 y − 3 + 1 z − 1 = 0 ⇔ 2 x − y + z = 0
H = d ∩ α ⇒ x − 1 2 = y + 1 − 1 = z − 3 1 = 2 x − 2 − y − 1 + z − 3 4 + 1 + 1 = 2 x − y + z − 6 6 = 0 − 6 6 = − 1
⇒ x = − 1 y = 0 z = 2 ⇒ H − 1 ; 0 ; 2
⇒ A H → − 2 ; − 3 ; 1
Δ 0 có 1 VTCP: u → = A H → ; n P → , với n P → = 1 ; 1 ; − 4
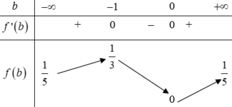
⇒ u → = 11 ; − 7 ; 1 ⇒ a = 11 ; b = − 7 ⇒ a + 2 b = − 3.
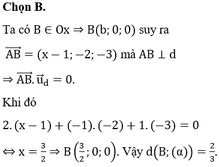
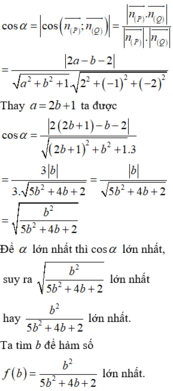
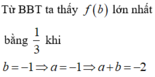
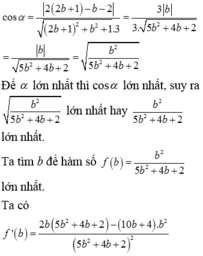
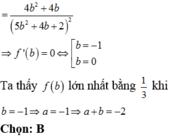
Chọn A