Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A.
Ta có
Suy ra phương trình mặt phẳng (ABC) là 5x -2y -z -6 =0
Do đó, điểm D(4;3;8) thuộc mặt phẳng (ABC).
Vậy có vô số mặt phẳng cách đều bốn điểm đã cho.
Đáp án D
Gọi I(a;b;c) là điểm cách đều bốn mặt phẳng (ABC), (BCD),(CDA), (DAB)
Khi đó, ta có
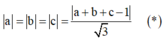
Suy ra có 8 cặp (a;b;c) thỏa mãn (*).
Đáp án B.
Kiểm tra ta được 4 điểm A, B, C, D không đồng phẳng nên tạo nên tứ diện.
- Một mặt phẳng đi qua A, B và song song với CD.
- Một mặt phẳng đi qua A, B và trung điểm CD.
Chọn D
Gọi điểm cần tìm là M (x0; y0; z0)
Phương trình mặt phẳng (ABC) là:
Phương trình mặt phẳng (BCD) là: x = 0
Phương trình mặt phẳng (CDA) là: y = 0
Phương trình mặt phẳng (DAB) là: z= 0.
Ta có M cách đều 4 mặt phẳng (ABC), (CDA), (BCD), (DAB) nên:
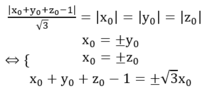
Ta có các trường hợp sau:
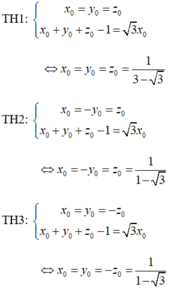
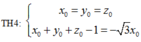
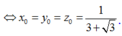
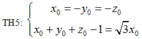
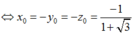
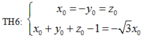
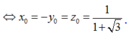
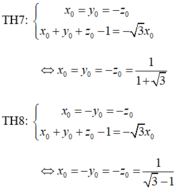
Vậy có 8 điểm M thỏa mãn bài toán.
Đáp án A
Phương pháp giải:
Xét vị trí tương đối của mặt phẳng, gọi phương trình tổng quát của mặt phẳng và tính toán dựa vào điều kiện tiếp xúc
Lời giải:
Gọi phương trình mặt phẳng cần tìm là (P): ax+by+cz+d=0
suy ra mp(P)//BC hoặc đi qua trung điểm của BC.
Mà B C → = ( - 4 ; 0 ; 0 ) và mp vuông góc với mp (Oyz) => (P) //BC
Với (P) //BC => a = 0 => by+cz+d=0
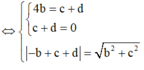
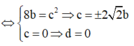
suy ra có ba mặt phẳng thỏa mãn
Đáp án D
Phương pháp :
Gọi (Q): x+y+z+a=0 a ≠ 0 là mặt phẳng song song với mặt phẳng (P).
Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.
Cách giải :
Gọi (Q): x+y+z+a=0 a ≠ 0 là mặt phẳng song song với mặt phẳng (P).
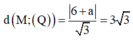
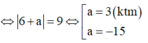
Vậy không có mặt phẳng (Q) nào thỏa mãn điều kiện bài toán.
Đáp án B
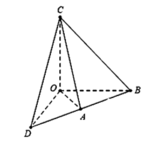
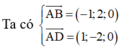
Do đó, 5 điểm O, A, B, C, D tạo thành tứ diện như hình vẽ bên
Vậy có tất cả 5 mặt phẳng cần tìm đó là:
Mặt phẳng (OAC) đi qua 3 điểm O, A, C
Bốn mặt phẳng là các mặt bên của tứ diện O.BCD đi qua 3 điểm trong 5 điểm O, A, B, C, D
Đáp án C
A B → = ( 1 ; - 1 ; - 3 ) , D C → = ( 1 ; - 1 ; - 3 ) , A D → = ( 2 ; - 4 ; - 2 ) => ABCD là hình bình hành
A B → . A D → . A E → = 12 ⇒ E . A B C D là hình chóp đáy hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên
+ Mặt phẳng qua 4 trung điểm lần lượt là AD, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt là EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt là EA, EB, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt là EA, ED, AB, DC
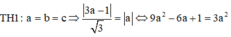
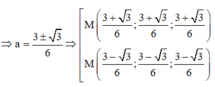
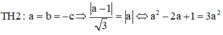
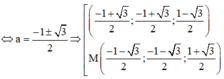
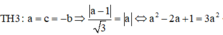
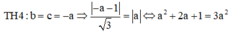
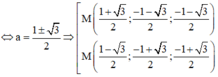
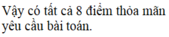
Chọn C
Ta có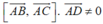
, suy ra bốn điểm A, B, C, D không đồng phẳng. Gọi (P) là mặt phẳng cách đều bốn điểm A, B, C, D.
TH1: Có một điểm nằm khác phía với ba điểm còn lại so với (P). Có bốn mặt phẳng thỏa mãn.
TH2: Mỗi phía của mặt phẳng (P) có hai điểm. Có ba mặt phẳng thỏa mãn.
Vậy có bảy mặt phẳng thỏa mãn.