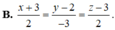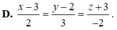Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Ta có: A (2; 0; 0), B (0; 4; 0), C (0; 0 ;6).
Thể tích khối tứ diện OABC là:
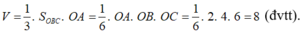

3.
\(d\left(I;\left(P\right)\right)=\frac{\left|-1-4-2-2\right|}{\sqrt{1^2+2^2+2^2}}=3\)
Áp dụng định lý Pitago:
\(R=\sqrt{5^2+3^2}=\sqrt{34}\)
Pt mặt cầu:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z+1\right)^2=34\)
\(\Leftrightarrow x^2+y^2+z^2+2x-4y+2z-28=0\)
4.
\(\left(\alpha\right)\) nhận \(\left(2;-3;-4\right)\) là 1 vtpt và tất cả các vecto có dạng \(\left(2k;-3k;-4k\right)\) cũng là các vecto pháp tuyến với \(k\ne0\) (bạn tự tìm đáp án phù hợp)
5.
\(\overrightarrow{AB}=\left(3;-6;0\right)\) ; \(\overrightarrow{AC}=\left(5;3;3\right)\)
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(-18;-9;39\right)=-3\left(6;3;-13\right)\)
Mặt phẳng (ABC) nhận \(\left(6;3;-13\right)\) là 1 vtpt
Phương trình:
\(6\left(x+1\right)+3\left(y-2\right)-13\left(z-3\right)=0\)
\(\Leftrightarrow6x+3y-13z+39=0\)
1.
\(\overrightarrow{IA}=\left(4;2;6\right)\Rightarrow R^2=IA^2=4^2+2^2+6^2=56\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y+3\right)^2+\left(z+2\right)^2=56\)
Dạng khai triển:
\(x^2+y^2+z^2-2x+6y+4z-42=0\)
2.
\(\overrightarrow{BA}=\left(10;2;-12\right)\Rightarrow R=\frac{AB}{2}=\frac{1}{2}\sqrt{10^2+2^2+12^2}=\sqrt{62}\)
Gọi I là trung điểm AB \(\Rightarrow I\left(1;1;1\right)\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=62\)
\(\Leftrightarrow x^2+y^2+z^2-2x-2y-2z-59=0\)

Đáp án D.
Mặt phẳng (P) có 1 vecto pháp tuyến n → = ( 6 ; 3 ; - 2 )
Đường thẳng AH qua A và vuông góc vưới (P)
Suy ra phương trình của đường thẳng AH là
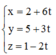
Suy ra H(2+6t; 5+3t; 1-2t)
Mà

Vậy H(-4;2;3)

Đáp án D.
Mặt phẳng (P) có 1 vecto pháp tuyến n → = ( 6 ; 3 ; - 2 )
Đường thẳng AH qua A và vuông góc vưới (P)
Suy ra phương trình của đường thẳng AH là

Suy ra H(2+6t; 5+3t; 1-2t)
Mà

Vậy H(-4;2;3)