Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Mặt phẳng (P): 3x – 3y + 2z - 5 = 0 có VTPT a → 3 ; - 3 ; 2

và đi qua A(-1;3;0)
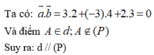


3(-1+2t) -3(3+4t) +2(3t) -5 =0 ⇒ 0t =17 ( vô nghiệm). Từ đó suy ra đường thẳng d song song với (P)

Chọn C.
Đường thẳng d có VTCP u → = 2 ; 1 ; 4 và đi qua M(1;7;3).
Đường thẳng d’ có VTCP u ' → = 3 ; - 2 ; 1 và đi qua N(6;-1;-2).


Đáp án A.
Đường thẳng d qua điểm M(2;-2;1) và có vectơ chỉ phương u → = ( - 3 ; 1 ; - 2 )
Đường thẳng d' qua điểm N(0;4;2) và có vectơ chỉ phương u ' → = 6 ; - 2 ; 4
Ta có
-
3
6
=
1
-
2
=
-
2
4
nếu
u
→
,
u
'
→
cùng phương. Lại có
M
2
;
-
2
;
-
1
![]()
Vậy d ∥ d '

Chọn B.
Đường thẳng d có VTCP ![]()
Đường thẳng d’ có VTCP ![]()
Từ đó ta có:
![]()
Lại có:
![]()
Suy ra d và d’ chéo nhau.

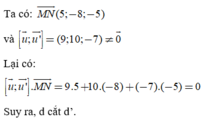



Chọn C.
Mặt phẳng (P): 3x + 5y – z – 2 = 0 có VTPT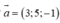
Đường thẳng