Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Phương pháp: Tâm đường tròn giao tuyến của mặt phẳng và mặt cầu là giao điểm của mặt phẳng đó và đường thẳng đi qua tâm mặt cầu vuông góc với mặt phẳng.
Cách giải: Phương trình đường thẳng d đi qua tâm mặt cầu (S) và vuông góc với mặt phẳng (P) là:
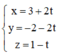
Tọa độ tâm đường tròn giao tuyến thỏa mãn hệ
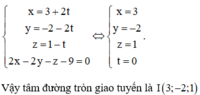
Chú ý: Bài toán cho vào trường hợp đặc biệt là tâm mặt cầu nằm trên mặt phẳng.
Đáp án A.
Giả sử mặt cầu (S) có tâm I a ; 0 ; 0 ∈ O x , bán kính R > 0 . Khi đó phương trình mặt cầu (S) là x − a 2 + y 2 + z 2 = R 2 .
Gọi H,K lần lượt là hình chiếu của I trên (P) và (Q) , khi đó:
I H = d I ; P = a + 1 6 và I K = d I ; Q = 2 a − 1 6
Do I H 2 + 4 = R 2 và I K 2 + r 2 = R 2 nên a + 1 2 6 + 4 = R 2 2 a − 1 2 6 + r 2 = R 2
⇒ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a + 1 2 + 24 = 2 a − 1 2 + 6 r 2
⇔ a 2 − 2 a + 2 r 2 − 8 = 0 *
Để có duy nhất một mặt cầu (S) thì phương trình (*) phải có một nghiệm
⇔ Δ ' = 1 − 2 r 2 − 8 = 0 ⇔ r 2 = 9 2 . Do r > 0 nên r = 3 2 .
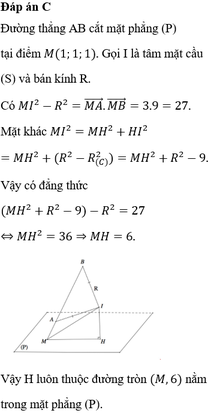
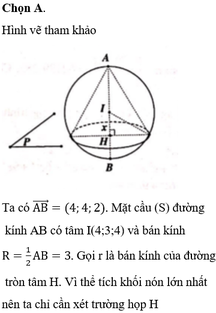
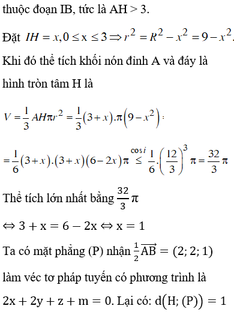
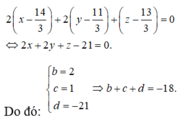
Đáp án A.
Phương pháp:
Mặt phẳng (P) cắt (S) theo một đường tròn (C) => Tâm H của (C) là hình chiếu của H trên (P).
Cách giải: Mặt cầu (S) có tâm I(1;2;3), bán kính R = 5
Mặt phẳng (P) cắt (S) theo một đường tròn (C) => Tâm H của (C) là hình chiếu của H trên (P)
Ta có n ( P ) → = ( 2 ; - 2 ; - 1 ) đường thẳng đi qua I và vuông góc với (P) có phương trình
Khi đó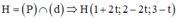
. Thay vào phương trình mặt phẳng (P) ta có: 2(1+2t) – 2(2–2t) – (3–t) – 4 = 0 ó 9t – 9 = 0 ó t = 1 ó H(3;0;2)