Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Giả sử mặt cầu (S) có tâm I a ; 0 ; 0 ∈ O x , bán kính R > 0 . Khi đó phương trình mặt cầu (S) là x − a 2 + y 2 + z 2 = R 2 .
Gọi H,K lần lượt là hình chiếu của I trên (P) và (Q) , khi đó:
I H = d I ; P = a + 1 6 và I K = d I ; Q = 2 a − 1 6
Do I H 2 + 4 = R 2 và I K 2 + r 2 = R 2 nên a + 1 2 6 + 4 = R 2 2 a − 1 2 6 + r 2 = R 2
⇒ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a + 1 2 + 24 = 2 a − 1 2 + 6 r 2
⇔ a 2 − 2 a + 2 r 2 − 8 = 0 *
Để có duy nhất một mặt cầu (S) thì phương trình (*) phải có một nghiệm
⇔ Δ ' = 1 − 2 r 2 − 8 = 0 ⇔ r 2 = 9 2 . Do r > 0 nên r = 3 2 .

Chọn đáp án D
Giả sử mặt cầu (S) có tâm I m ; 0 ; 0 và bán kính là R (do I ∈ O x ).
Ta có
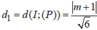
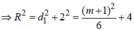
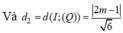
![]()
Từ đó suy ra
![]()
![]()
Để có đúng một mặt cầu (S) thỏa mãn yêu cầu khi và chỉ khi phương trình (*) có đúng một nghiệm m, tức là
![]()
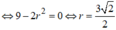

Đáp án D.
Gọi I a ; 0 ; 0 là tâm của mặt cầu (S) có bán kính R.
Khoảng cách từ tâm I đến hai mặt phẳng (P) và (Q) lần lượt là d 1 = a + 1 6 , d 2 = 2 a + 1 6
Theo giả thiết, ta có:
R 2 = d 1 2 + 2 2 = d 2 2 + r 2 ⇔ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a 2 + 2 a + 25 = 4 a 2 − 4 a + 1 + 6 r 2 ⇔ 3 a 2 − 6 a + 6 r 2 − 24 = 0 *
Yêu cầu bài toán (*) có nghiệm duy nhất
⇔ Δ ' = − 3 2 − 3 6 r 2 − 24 = 0 ⇔ r = 3 2 2 .

Đáp án B
Mặt cầu (S) có tâm I(1;-1;2) và bán kính ![]()
Ta có (Q) // (P) nên (Q) có dạng: ![]()
Mặt phẳng (Q) cắt (S) theo 1 đường tròn có bán kính
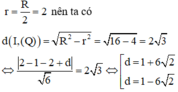
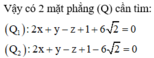

Gọi H,I lần lượt là hình chiếu vuông góc của O lên (P) và ∆ .
Ta có d ( O; ∆ ) = OI ≥ OH. Dấu “=” xảy ra khi I = H.
Đường thẳng OH qua O ( 0;0;0 ) nhận n → = ( 1;2;1 ) làm vectơ chỉ phương nên có phương trình là x = t y = 2 t z = t
Mặt phẳng (P) có phương trình: x + 2y + z - 6 = 0.
Từ hai phương trình trên suy ra t = 1 nên H ( 1;2;1 ).
Khi đó (Q) là mặt phẳng chứa d và đi qua H.
Ta có M ( 1;1;2 ) ∈ d , vectơ chỉ phương của d là u → = ( 1;1;-2 ); H M → = ( 0;-1;1 ).
Suy ra vectơ pháp tuyến của (Q) là n → = n → ; H M → = ( -1;-1;-1 ) . Hơn nữa (Q) qua điểm M ( 1;1;2 ) nên (Q) có phương trình là:x + y + z - 4 = 0
Đáp án C

Chọn C.
Phương pháp: Lần lượt tìm các yếu tố tâm và bán kính của mặt cầu.
Cách giải: Tọa độ tâm mặt cầu thỏa mãn hệ

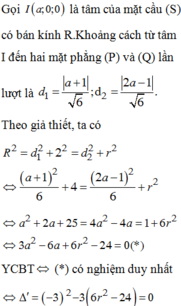
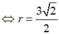

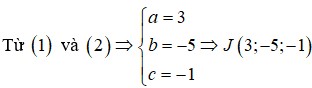


Đáp án D
Phương pháp: d 2 + r 2 = R 2
Trong đó,
d: khoảng cách từ tâm O đến mặt phẳng (P),
r: bán kính đường tròn là giao tuyến của mặt cầu (S)
và mặt phẳng (P),
R: bán kính hình cầu.
Cách giải:
(S): x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 5 = 0 <=> x - 3 2 + y + 2 2 + z - 1 2 = 9
=> (S) có tâm I(3; –2;1) bán kính R = 3
(Q) cắt (S) theo giao tuyến là một đường tròn bán kính r = 2
Ta có: d 2 + r 2 = R 2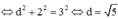
Gọi n → a ; b ; c , n → ≠ 0 là một VTPT của (Q). Khi đó n → vuông góc với VTCP n → 1 ; 0 ; 0 của Ox
=>1.a + 0.b +).c = 0 ó a = 0
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT n → 0 ; b ; c , n → ≠ 0 là:
0.(x – 0) + b(y – 0) + c(z – 0) ó by + cz = 0
Khoảng cách từ tâm I đến (Q):
Cho c = –1 => b = 2 => n → 0 ; 2 ; - 1
Phương trình mặt phẳng (Q): 2y - z = 0