Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi tâm mặt cầu là I(a;b;c). Vì mặt cầu tiếp xúc với cả ba mặt phẳng (P);(Q);(R) nên ta có
![]()
Hay |a-1|=|b+1|=|c-1|=R
Vì mặt cầu tiếp xúc với cả ba mặt phẳng nên ta có điều kiện a > 1 b < - 1 c > 1
Suy ra a-1= -1-b=c-1 ⇔ -a=b=-c
⇒ I(a;-a;a)
Mà A ∈ S nên IA=R=|a-1|
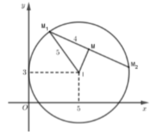
Ta có
![]()
![]()
![]()
⇔ a = 4 ⇒ R = 3
Chọn đáp án A.

HD: Dễ thấy (P)//(Q). Gọi (R) là mặt phẳng song song và cách đều 2 mặt phằng (P) và (Q)



Đáp án A.
Giả sử mặt cầu (S) có tâm I a ; 0 ; 0 ∈ O x , bán kính R > 0 . Khi đó phương trình mặt cầu (S) là x − a 2 + y 2 + z 2 = R 2 .
Gọi H,K lần lượt là hình chiếu của I trên (P) và (Q) , khi đó:
I H = d I ; P = a + 1 6 và I K = d I ; Q = 2 a − 1 6
Do I H 2 + 4 = R 2 và I K 2 + r 2 = R 2 nên a + 1 2 6 + 4 = R 2 2 a − 1 2 6 + r 2 = R 2
⇒ a + 1 2 6 + 4 = 2 a − 1 2 6 + r 2 ⇔ a + 1 2 + 24 = 2 a − 1 2 + 6 r 2
⇔ a 2 − 2 a + 2 r 2 − 8 = 0 *
Để có duy nhất một mặt cầu (S) thì phương trình (*) phải có một nghiệm
⇔ Δ ' = 1 − 2 r 2 − 8 = 0 ⇔ r 2 = 9 2 . Do r > 0 nên r = 3 2 .

Chọn C.
Phương pháp: Lần lượt tìm các yếu tố tâm và bán kính của mặt cầu.
Cách giải: Tọa độ tâm mặt cầu thỏa mãn hệ





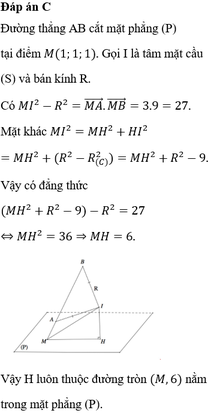

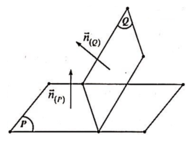
Chọn đáp án B.