

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Phương pháp giải: Áp dụng ứng dụng của tích có hướng trong không gian
Lời giải:
![]()
![]()
Suy ra
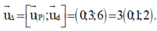
![]()

Đáp án C
Ta có VTCP (P): n → (1; -2; 3), do d vuông góc với (P) nên u d → = (1; -2; 3)

Đáp án C
Vì d ⊥ ( P ) suy ra u d → = n ( P ) → = ( 4 ; 0 ; - 1 )

Chọn C
Ta có mặt phẳng α nhận vectơ n α → = ( 1 ; 1 ; 1 ) là vectơ pháp tuyến, đường thẳng d đi qua điểm A(0;-1;2) và nhận u d → = ( 1 ; 2 ; - 1 ) là vectơ chỉ phương.
Gọi β là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng α
![]()
Khi đó đường thẳng ∆ là giao tuyến của hai mặt phẳng α và β . Do đó một vectơ chỉ phương của đường thẳng ∆ là .
![]()
Mà u → = ( 1 ; a ; b ) nên a=4, b = -5 => a+b = 4-5 =-1.

Đáp án C
Mặt phẳng (P) có một véc-tơ pháp tuyến là ![]() =(4;0;-1),
=(4;0;-1),
do đường thẳng ![]() , nên véc-tơ pháp tuyến của mặt phẳng (P) cũng là véc-tơ chỉ phương của đường thẳng d.
, nên véc-tơ pháp tuyến của mặt phẳng (P) cũng là véc-tơ chỉ phương của đường thẳng d.