Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Giả sử A (a; 0; 0), B (0; b; 0), C (0; 0; c) với a, b, c ≠ 0
Phương trình mặt phẳng (P) qua A, B, C có dạng: ![]()
Vì (P) đi qua M (3; 2; 1) nên ta có: 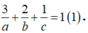

Vậy phương trình mặt phẳng (P):
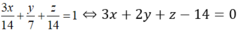

Đáp án C
Cách giải:
Gọi tọa độ các giao điểm
![]()
Khi đó phương trình mặt phẳng (P) có dạng đoạn chắn
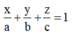
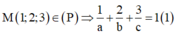
Vì OA=2OB=3OC>0 nên
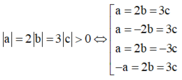
TH1: a=2b=3c
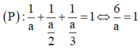
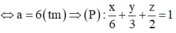
TH2: a=-2b=3c
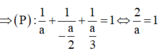
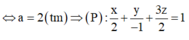
TH3: a=2b=-3c
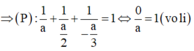
TH1: -a=2b=3c
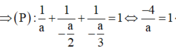
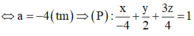
Vậy, có 3 mặt phẳng (P) thỏa mãn yêu cầu đề bài.

Chọn D
Gọi A (a;0;0), B (0;b;0); C (0;0;c). Ta có OA = |a|; |OB| = b; |OC| = |c|.
Phương trình mặt phẳng đi qua ba điểm A, B, C là ![]()
Theo giả thiết ta có điểm 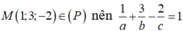
Vì OA=OB=OC => |a| = |b| = |c| nên ta có hệ phương trình
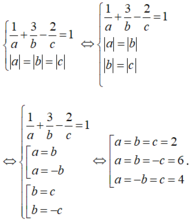
Vậy có 3 mặt phẳng thỏa mãn.

Đáp án D
Phương pháp
Gọi A(a;0;0), B(0;b;0), C(0;0;c)
![]()
Chia các trường hợp để phá trị tuyệt đối và viết phương trình mặt phẳng (P) dạng đoạn chắn.
Cách giải: Giả sử A(a;0;0), B(0;b;0), C(0;0;c)
![]()
![]()
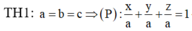
![]()
![]()
![]()
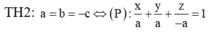
![]()
![]()
![]()
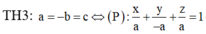
![]()
![]()
![]()

![]()
![]()
![]()
Vậy có 4 mặt phẳng thỏa mãn yêu cầu bài toán.

Đáp án D
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC (M là trực tâm tam giác ABC) nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: n p → = OM → = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0

Đáp án D
Ta có OA ⊥ OB, OC => OA ⊥ (OBC) => OA ⊥ BC.
Mặt khác ta có AM ⊥ BC nên ta suy ra BC ⊥ (OAM) => BC ⊥ OM
Chứng minh tương tự ta được AC ⊥ OM. Do đó OM ⊥ (ABC).
Ta chọn n P → = OM → = (1; 2; 2). Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) + 2(y - 2) + 2(z - 2) = 0 <=> x + 2y + 2z - 9 = 0
Chọn D

a. Mặt phẳng (P) có (3;-2;2) là 1 vtpt nên d nhận (3;-2;2) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+3t\\y=2-2t\\z=-1+2t\end{matrix}\right.\)
b. \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\) ; \(\overrightarrow{n_{\left(P'\right)}}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(P'\right)}}\right]=\left(2;0;-2\right)=2\left(1;0;-1\right)\)
\(\Rightarrow\) d nhận (1;0;-1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=-2\\z=3-t\end{matrix}\right.\)
c. \(\overrightarrow{u_{\Delta}}=\left(3;2;1\right)\) ; \(\overrightarrow{u_{\Delta'}}=\left(1;3;-2\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{u_{\Delta'}}\right]=\left(-7;7;7\right)=7\left(-1;1;1\right)\)
Đường thẳng d nhận (-1;1;1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=-1-t\\y=1+t\\z=3+t\end{matrix}\right.\)

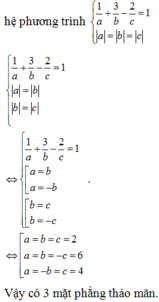

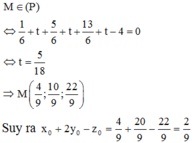
Đáp án B.
Do M là trực tâm của tam giác ABC nên: CM ⊥ AB lại có
Suy ra (ABC): 3x+y+z-14=0