
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

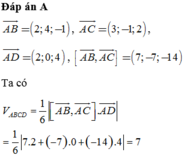

\(\left\{{}\begin{matrix}a+8-c+d=0\\\dfrac{\left|a-8+2c+d\right|}{\sqrt{a^2+16+c^2}}=5\end{matrix}\right.\)
\(\Rightarrow\left(3c-16\right)^2=25\left(a^2+c^2+16\right)\)
\(\Rightarrow25a^2+16c^2+96c+144=0\)
\(\Rightarrow25a^2+16\left(c+3\right)^2=0\Rightarrow\left\{{}\begin{matrix}a=0\\c=-3\end{matrix}\right.\)
\(\Rightarrow d=c-a-8=-11\)
\(\Rightarrow a+c+d=-14\)

Chọn B
Ta có d₁ đi qua điểm M (1;2;-3) và có vtcp ![]()
Đường thẳng d₂ đi qua điểm N (4;3;1) và có vtcp ![]()
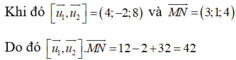
nên hai đường thẳng đã cho luôn chéo nhau và
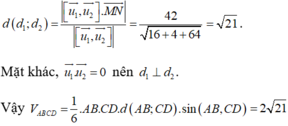

Chọn B
Mặt phẳng (ABC) đi qua B (1; 0; -1) và có một véctơ pháp tuyến là:
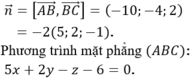
Phương trình mặt phẳng (ABC): 5x + 2y - z - 6 = 0
Độ dài đường cao xuất phát từ đỉnh D (0; 0; d) của tứ diện ABCD bằng d(D, (ABC))
Theo bài ra ta có:
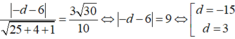
Do D thuộc tia Oz nên D (0; 0; 3).

Chọn D
Trên cạnh AB, AC , AD của tứ diện ABCD lần lượt có các điểm B', C', D'. Áp dụng công thức tỷ số thể tích ta có
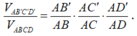
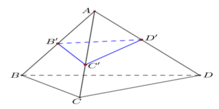
Từ giả thiết
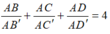
áp dụng bất đẳng thức AM- GM ta có
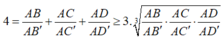
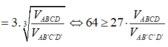
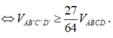
Do thể tích ABCD cố định nên thể tích AB'C'D' nhỏ nhất
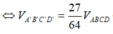
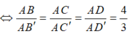
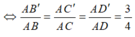
=> (B'C'D') song song với (BCD) và đi qua điểm B'
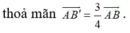
![]()
![]()
suy ra vectơ pháp tuyến của mặt phẳng (B'C'D') là:
![]()
![]()
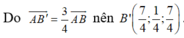
Vậy phương trình (B'C'D') là:
![]()

Do (P) song song (Q) \(\Rightarrow\left\{{}\begin{matrix}b=1\\c=-3\end{matrix}\right.\) \(\Rightarrow x+y-3z+d=0\) với \(d\ne4\)
\(d\left(M;\left(P\right)\right)=d\left(N;\left(P\right)\right)\Rightarrow\dfrac{\left|1+6+21+d\right|}{\sqrt{1^2+1^2+\left(-3\right)^2}}=\dfrac{\left|5+0+3+d\right|}{\sqrt{1^2+1^2+\left(-3\right)^2}}\)
\(\Rightarrow\left|d+28\right|=\left|d+8\right|\Rightarrow d=-18\)
\(\Rightarrow b+c+d=-20\)

6.
Mặt phẳng Oxz có pt: \(y=0\)
Khoảng cách từ I đến Oxz: \(d\left(I;Oxz\right)=\left|y_I\right|=2\)
\(\Rightarrow R=2\)
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=4\)
7.
Mặt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên cũng nhận các vecto có dạng \(\left(k;-2k;3k\right)\) là vtpt
Bạn có ghi nhầm đề bài ko nhỉ? Thế này thì cả C và D đều ko phải vecto pháp tuyến của (Q)
4.
Đường thẳng d nhận \(\left(1;-2;2\right)\) là 1 vtcp
Gọi (P) là mặt phẳng qua M và vuông góc d \(\Rightarrow\) (P) nhận \(\left(1;-2;2\right)\) là 1 vtpt
Phương trình (P): \(1\left(x-2\right)-2\left(y-3\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x-2y+2z+6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=4+t\\y=1-2t\\z=5+2t\end{matrix}\right.\)
Tọa độ hình chiếu M' của M lên d là giao của d và (P) nên thỏa mãn:
\(4+t-2\left(1-2t\right)+2\left(5+2t\right)+6=0\) \(\Rightarrow t=-2\)
\(\Rightarrow M'\left(2;5;1\right)\)
5.
(P) nhận \(\left(2;3;1\right)\) là 1 vtpt
Gọi d là đường thẳng qua I và vuông góc (P)
\(\Rightarrow\) d nhận \(\left(2;3;1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+2t\\y=-2+3t\\z=1+t\end{matrix}\right.\)
H là giao điểm của d và (P) nên tọa độ thỏa mãn:
\(2\left(1+2t\right)+3\left(-2+3t\right)+1+t-11=0\) \(\Rightarrow t=1\)
\(\Rightarrow H\left(3;1;2\right)\)