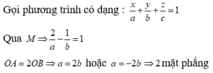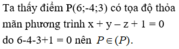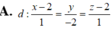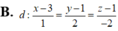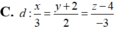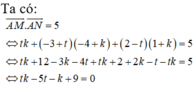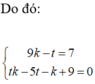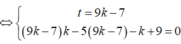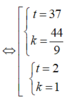Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Do (P) ⊥ AB nên mp(P) có một vectơ pháp tuyến là n P → = AB → = (-2; 1; 3). Mặt khác (P) đi qua điểm A nên phương trình của mặt phẳng (P) là:
-2(x - 1) + (y - 0) + 3(z + 2) = 0 ⇔ -2x + y + 3z + 8 = 0 ⇔ 2x - y - 3z - 8 = 0.
Vậy đáp án đúng là A.
Lưu ý. Khi ta viết phương trình mặt phẳng (P) bị nhầm ở cột z:
-2(x - 1) + (y - 0) + 3(z + 2) = 0 <> 2x - y - 3z - 4 = 0
thì ta được đáp án B.
Khi ta viết phương trình mặt phẳng bị nhầm giữa tọa độ của điểm A với tọa độ của vectơ pháp tuyến 1(x - (-2)) + 0(y - 1) -2(z - 3) = 0 <=> x - 2x + 8 = 0 thì ta được đáp án C.
Khi ta viết phương trình mặt phẳng đi qua B thì ta thu được đáp án D.

Mặt cầu (S) có tâm I(-2;-1;1) và bán kính \(R=\sqrt{5}\)
Gọi r là bán kinh đường tròn thiết diện, theo giả thiết ta có : \(S=\pi\Leftrightarrow r^2.\pi=\pi\Rightarrow r=1\)
Gọi d là khoảng cách từ I đến mặt phẳng \(\alpha\), ta có \(d^2=R^2-r^2=5-1\Rightarrow d=2\)
Mặt phẳng \(\alpha\), qua N (0;-1;0) có dạng \(Ax+B\left(y+1\right)+Cz=0\Leftrightarrow Ax+By+Cz+B=0\left(A^2+B^2+C^2\ne0\right)\)
Mặt khác, \(\alpha\) qua M(1;-1;1) nên thỏa mãn \(A+C=0\Rightarrow\text{ }\) \(\alpha:Ax+By-Az+B=0\)
Vì \(d=d\left(I,\alpha\right)=\frac{\left|-3A\right|}{\sqrt{2A^2+B^2}}=2\Leftrightarrow A^2=4B^2\Rightarrow\frac{A}{B}=\pm2\) vì \(A^2+B^2+C^2\ne0\)
Do đó có 2 mặt phẳng \(\alpha\), cần tìm là \(2x+y-2z+1=0\) và \(2x-y-2z-1=0\)

Đáp án B.
Phương pháp giải: Gọi tọa độ điểm, tính khoảng cách và tìm tọa độ tâm thông qua bán kính
Lời giải: Ta có
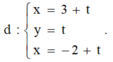
![]()
![]()
![]()

Phương trình mặt phẳng (Oxy): z=0
Khoảng cách từ tâm I đến mp(Oxy) là
![]()
Theo bài ra, ta có
![]()
![]()
![]()

Gọi Q là mặt phẳng đi qua A và song song với (P) thì phương trình của (Q) là \(\left(x+2\right)+2\left(y+1\right)-\left(z-1\right)=0\) hay \(x+2y-z+5=0\). Gọi H là hình chiếu vuông góc của B lên (Q). Giả sử \(\Delta\) là đường thẳng qua A và song song với