Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Xét khẳng định C:
Nếu đường thẳng d đi qua gốc tọa độ O thì đường thẳng d có vectơ chỉ phương là OM → = (2; -1; 1)
Do u d → . n p → = 2.1 - 1.1 + 1.1 = 2 ≠ 0 nên đường thẳng d không song song với mặt phẳng (P)
(mâu thuẫn giả thiết)
Vậy khẳng định C là sai.

Đáp án A
Vì đường thẳng d vuông góc với mặt phẳng (Oxy) nên đường thẳng d có vectơ chỉ phương là (0 ;0 ;1). Từ đó suy ra A là khẳng định sai.

Đáp án A
Do đường thẳng d song song với hai mặt phẳng (Oxy) và (Oxz).
Lại có: (Oxy) ∩ (Oxz) = Ox
Suy ra đường thẳng d song song với trục Ox.
Kết hợp với điểm O thuộc Ox, ta suy ra đường thẳng d không thể đi qua điểm O với mọi m. Vậy A là khẳng định sai.

Đáp án D
Ta có:
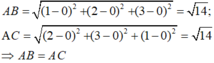
Ta thấy tam giác ABC cân tại đỉnh A. Do đó, AD đồng thời là đường cao của tam giác ABC nên các khẳng định A, B và C đều đúng.
Vậy khẳng định D sai.

Đáp án A
Ta có: ![]()
AM → (3; 2; 4)
Mặt phẳng (P) có vecto pháp tuyến là n p → (1; 1; 1)
Gọi H là hình chiếu vuông góc của A trên d. Ta có: d(A; d) = AH ≤ AM = 29
Dấu bằng xảy ra khi và chỉ khi H trùng M, nghĩa là d vuông góc với AM.
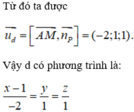

`a)` Vì `AM` là đường trung tuyến của `\triangle ABC`
`=>M` là trung điểm của `BC`
`=> M ( 1 ; -2 )`
Ta có: `\vec{AM} = ( -1 ; -2 )`
`=>\vec{n_[AM]} = ( 2 ; -1 )`
Mà `A ( 2 ; 0 ) in AM`
`=>` Ptr đường trung tuyến `AM` là: `2 ( x - 2 ) - ( y - 0 ) = 0`
`<=> 2x - y - 4 = 0`
________________________________________________________
`b)` Ta có: `\vec{AC} = ( -2 ; -1 )`
Gọi ptr đường thẳng vuông góc với `AC` là `\Delta`
`=>` Ptr `\Delta` là: `-2x - y + c = 0`
`d ( B , \Delta ) = \sqrt{5}`
`=> [ | -2 . 2 - (-3) + c | ] / \sqrt{(-2)^2 + (-1)^2} = \sqrt{5}`
`<=> | c - 1 | = 5`
`<=> c = 6` hoặc `c = -4`
`=>` Ptr `\Delta` là: `-2x - y + 6 = 0`
hoặc `-2x - y - 4 = 0`

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
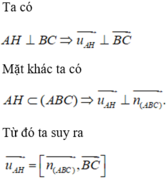
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

a: Tọa độ trọng tâm là:
x=(1+2+0)/3=1 và y=(3+1+3)/3=7/3
c: \(d\left(A;d\right)=\dfrac{\left|1\cdot1+3\cdot\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)
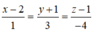
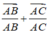
Đáp án D