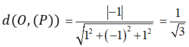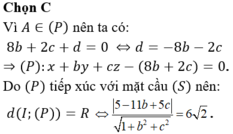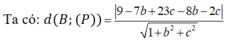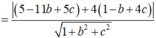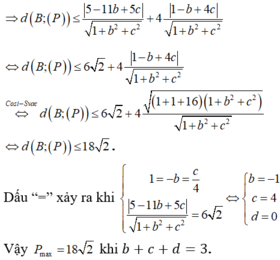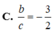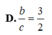Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}a+8-c+d=0\\\dfrac{\left|a-8+2c+d\right|}{\sqrt{a^2+16+c^2}}=5\end{matrix}\right.\)
\(\Rightarrow\left(3c-16\right)^2=25\left(a^2+c^2+16\right)\)
\(\Rightarrow25a^2+16c^2+96c+144=0\)
\(\Rightarrow25a^2+16\left(c+3\right)^2=0\Rightarrow\left\{{}\begin{matrix}a=0\\c=-3\end{matrix}\right.\)
\(\Rightarrow d=c-a-8=-11\)
\(\Rightarrow a+c+d=-14\)

\(\overrightarrow{AB}=\left(8;0;-2\right)=2\left(4;0;-1\right)\)
Phương trình AB có dạng: \(\left\{{}\begin{matrix}x=5+4t\\y=2\\z=2-t\end{matrix}\right.\)
Tọa độ M thỏa mãn:
\(5+4t+2-3\left(2-t\right)+4=0\) \(\Rightarrow t=-\dfrac{5}{7}\)
\(\Rightarrow M\left(\dfrac{15}{7};2;\dfrac{19}{7}\right)\) \(\Rightarrow\left\{{}\begin{matrix}MA=\dfrac{9\sqrt{17}}{7}\\MB=\dfrac{5\sqrt{17}}{7}\end{matrix}\right.\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{9}{5}\)

Do (P) song song (Q) \(\Rightarrow\left\{{}\begin{matrix}b=1\\c=-3\end{matrix}\right.\) \(\Rightarrow x+y-3z+d=0\) với \(d\ne4\)
\(d\left(M;\left(P\right)\right)=d\left(N;\left(P\right)\right)\Rightarrow\dfrac{\left|1+6+21+d\right|}{\sqrt{1^2+1^2+\left(-3\right)^2}}=\dfrac{\left|5+0+3+d\right|}{\sqrt{1^2+1^2+\left(-3\right)^2}}\)
\(\Rightarrow\left|d+28\right|=\left|d+8\right|\Rightarrow d=-18\)
\(\Rightarrow b+c+d=-20\)

Chọn D
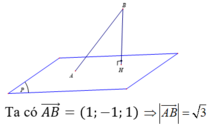
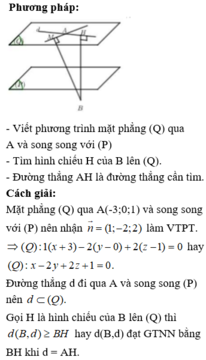
Gọi H là hình chiếu của B trên mặt phẳng (P) khi đó ta có BH là khoảng cách từ điểm B đến mặt phẳng (P). Ta luôn có BH ≤ AB do đó khoảng cách từ B đến mặt phẳng (P) lớn nhất khi H ≡ A, khi đó ![]() là véc tơ pháp tuyến của mặt phẳng (P)
là véc tơ pháp tuyến của mặt phẳng (P)
Vậy phương trình mặt phẳng (P) đi qua A (-1; 2; 4) và có véc tơ pháp tuyến ![]() là x - y + z - 1 = 0
là x - y + z - 1 = 0
Vậy khoảng cách từ điểm O đến mặt phẳng (P) là: