Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
![]()
![]()
Vì M là hình chiếu vuông góc của I trên ∆
![]()
Khi đó
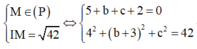
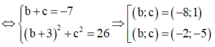
Vậy M(5;-2;-5) hoặc M(5;-8;1) => bc =10

Chọn A
Ta có 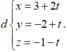 Vì M là giao điểmcủa d và (P) nên ta có tọa độ của M cũng thỏa mãn phương trình mặt phẳng (P) hay
Vì M là giao điểmcủa d và (P) nên ta có tọa độ của M cũng thỏa mãn phương trình mặt phẳng (P) hay

Gọi điểm H là hình chiếu của M lên
đường thẳng ∆ ta có
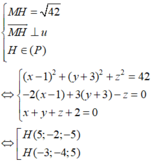
Vậy tồn tại hai đường thẳng ∆ thỏa mãn đề bài

Bài này cần có 1 điều gì đó đặc biệt trong các đường - mặt để giải được (nếu ko chỉ dựa trên khoảng cách thông thường thì gần như bất lực). Thường khoảng cách dính tới đường vuông góc chung, thử mò dựa trên nó :)
Bây giờ chúng ta đi tìm đường vuông góc chung d3 của d1; d2, và hi vọng rằng giao điểm C của d3 với (P) sẽ là 1 điểm nằm giữa A và B với A và giao của d1 và d3, B là giao của d2 và d3 (nằm giữa chứ ko cần trung điểm), thường ý tưởng của người ra đề sẽ là như vậy. Khi đó điểm M sẽ trùng C. Còn C không nằm giữa A và B mà nằm ngoài thì đầu hàng cho đỡ mất thời gian (khi đó việc tìm cực trị sẽ rất lâu).
Quy pt d1 và d2 về dạng tham số, gọi A là 1 điểm thuộc d1 thì \(A\left(t+1;t+2;2t\right)\) và B là 1 điểm thuộc d2 thì \(B\left(t'+1;2t'+3;3t'+4\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(t'-t;2t'-t+1;3t'-2t+4\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}.\overrightarrow{u_{d1}}=0\\\overrightarrow{AB}.\overrightarrow{u_{d2}}=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}t'-t+2t'-t+1+2\left(3t'-2t+4\right)=0\\t'-t+2\left(2t'-t+1\right)+3\left(3t'-2t+4\right)=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}t=0\\t'=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(1;2;0\right)\\B\left(0;1;1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{BA}=\left(1;1-1\right)\)
Phương trình AB hay d3: \(\left\{{}\begin{matrix}x=1+t\\y=2+t\\z=-t\end{matrix}\right.\)
Giao điểm C của d3 và (P): \(2\left(1+t\right)+2\left(2+t\right)-2t-5=0\)
\(\Rightarrow C\left(\dfrac{1}{2};\dfrac{3}{2};\dfrac{1}{2}\right)\)
Ủa, ko chỉ nằm giữa luôn, mà người ta cho hẳn trung điểm cho cẩn thận :)
Vậy \(M\left(\dfrac{1}{2};\dfrac{3}{2};\dfrac{1}{2}\right)\)

Chọn D
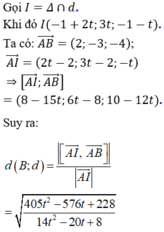
Xét hàm số:
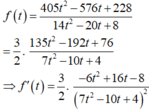
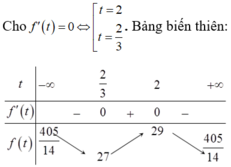
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra ![]() . Chọn một vectơ chỉ phương của đường thẳng d là
. Chọn một vectơ chỉ phương của đường thẳng d là ![]()
Vậy phương trình đường thẳng ![]()

Đáp án C
Gọi H là hình chiếu của M trên (P) => MH là khoảng cách từ M đến mặt phẳng (P). Đường thẳng D có vectơ chỉ phương u → =(2;1;3) mặt phẳng (P) có vectơ pháp tuyến n → =(1;1;-2)
Khi đó:
![]()
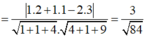
Tam giác MHA vuông tại H




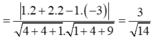

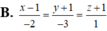

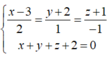
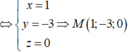
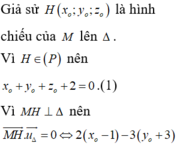
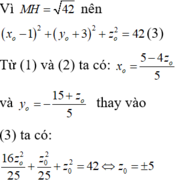

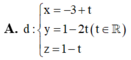
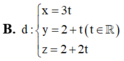
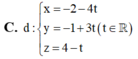
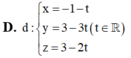

I là giao điểm của d và P nên tọa độ của I sẽ là:
1+2t+2(1+2t)+2t+1=0 ⇔ t = -0,5
thay t=-0,5 vào d ta đc x=0; y=0; z=-1/2
=> I(0;0;-1/2)
Gọi tọa độ M là (x;y;z) :
\(\overrightarrow{IM}\) = (x;y;z+\(\dfrac{1}{2}\)) mà IM=9 ⇔ \(\sqrt{x^2+y^2+\left(z+\dfrac{1}{2}\right)^2}\)=9
⇔\(x^2+y^2+\left(z+\dfrac{1}{2}\right)^2=81\)
thay tọa độ x, y, z ở đường thẳng d vào ta đc:
\(\left(1+2t\right)^2+\left(1+2t\right)^2+\left(t+\dfrac{1}{2}\right)^2\)=81.
=> \(\left[{}\begin{matrix}t=2,5\\t=-3,5\end{matrix}\right.\)
thay 1 trong 2 giá trị của t vào phương trình đt d. tớ sẽ thay t=2.5
=> M(6;6;2,5)
\(d\left(M,\left(P\right)\right)=\dfrac{\left|6+12+5+1\right|}{3}\) = 8
câu B đúng