Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

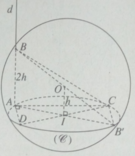
Tam giác ADC vuông tại A nên AD 2 = DC 2 - AC 2 (1)
Tam giác ABC vuông tại A nên BC 2 = AC 2 + AB 2 (2)
Từ (1) và (2) ta suy ra AD 2 + BC 2 = DC 2 + AB 2 (3)
Ta lại có:
AC 2 = DC 2 - AD 2 và BD 2 = AD 2 + AB 2 (4)
DC 2 = 4 r 2 - h 2 , AB 2 = 4 h 2 (5)
Từ (4) và (5) ta có:
AC 2 + BD 2 = DC 2 + AB 2 = 4 r 2 - h 2 + 4 h 2 = 4 r 2 (6)
Từ (3) và (6) ta có: AD 2 + BC 2 = AC 2 + BD 2 (không đổi)

Đáp án A
Từ vị trí tương đối của một đường thẳng và mặt cầu ta có đường thẳng d có điểm chung với mặt cầu (S) khi và chỉ khi đường thẳng d tiếp xúc hoặc cắt mặt cầu (S).

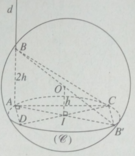
Diện tích tam giác BCD bằng:
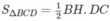
Diện tích này lớn nhất khi AI // CD.

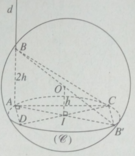
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).

Chọn A
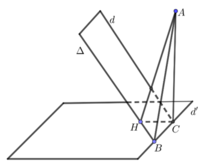
Cách 1: Ta có: B ∈ Oxy và B ∈ (α) nên B (a ; 2 – 2a ; 0).
![]() đi qua M (-1 ; -2 ; -3) và có một véctơ chỉ phương là
đi qua M (-1 ; -2 ; -3) và có một véctơ chỉ phương là ![]()
Ta có: d ⊂ (α) nên d và Δ song song với nhau và cùng nằm trong mặt phẳng (α).
Gọi C = d ∩ (Oxy) nên 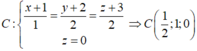
Gọi d’ = (α) ∩ (Oxy), suy ra d’ thỏa hệ 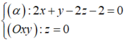
Do đó, d’ qua 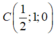 và có VTCP
và có VTCP ![]()
Gọi φ = (Δ, d’) = (d, d’)
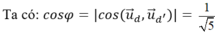
Gọi H là hình chiếu của C lên Δ. Ta có CH = 3 và 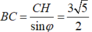
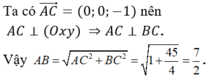
Cách 2: Ta có: ![]() đi qua M (-1 ; -2 ; -3) và có một VTCP là
đi qua M (-1 ; -2 ; -3) và có một VTCP là ![]()
Ta có: B = Δ ∩ (Oxy), Δ ⊂ (α) nên B ∈ (Oxy) ∩ (α) => B (a; 2 – a; 0)
Ta có: Δ // d và d (Δ, d) = 3 nên 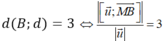
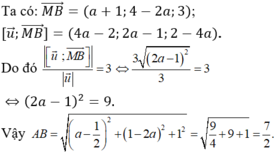
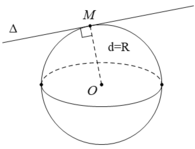
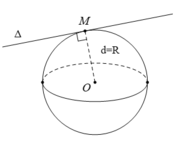
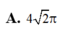
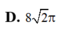
Đáp án C