Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ lúc 12 giờ đến 15 giờ kim giờ quay được 1 góc 90o
Từ lúc 12 giờ đến 15 giờ kim phút quay được 1 góc: 3 vòng. 360o=1080o

Tham khảo:
a) Số xe trung bình đi qua trạm thu phí trong mỗi phút là: \(\bar x \approx 17,4\) (xe).
b)

c) Do số xe là số nguyên nên ta hiệu chỉnh lại như sau:

Số xe trung bình đi qua trạm thu phí trong mỗi phút từ bảng tần số ghép nhóm là:
\(\bar x = \frac{{5.8 + 9.13 + 3.18 + 9.23 + 4.28}}{{30}} \approx 17,7\)

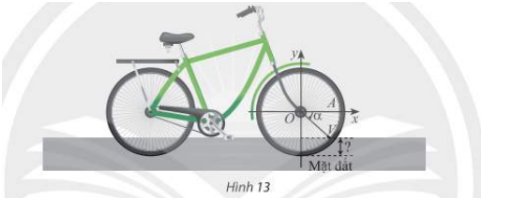
Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)

Sau 1 phút cả 2 máy bay bay được quãng đường dài \(1.v = v\)
Áp dụng công thức tính độ cao của máy bay so với mặt đất, ta tính được độ cao của hai máy bay 1 và 2 như sau:
Độ cao của máy bay 1: \({h_1} = v.\sin {10^0} \approx 0,17v\)
Độ cao của máy bay 2: \({h_2} = v.\sin {15^0} \approx 0,26v\)
Do đó, ta thấy rằng độ cao của máy bay 2 lớn hơn độ cao của máy bay 1. Vì vậy, máy bay 2 ở độ cao so với mặt đất lớn hơn sau 1 phút kể từ khi cất cánh.

Lời giải:
Thời gian người đó đi quãng đường AB:
8 giờ 45 phút - 6 giờ 15 phút = 2 giờ 30 phút = 2,5 giờ
Vận tốc trung bình của ô tô:
$120:2,5=48$ (km/h)

Hàm số \(T\left( t \right)\) có tập xác định là \(\left[ {0;100} \right]\).
Ta có: \(T\left( {60} \right) = 10 + 2.60 = 130\)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ + }} \left( {k - 3t} \right) = k - 3.60 = k - 180\\\mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} \left( {10 + 2t} \right) = 10 + 2.60 = 130\end{array}\)
Để hàm số liên tục trên tập xác định thì hàm số phải liên tục tại điểm \({t_0} = 60\)
Khi đó: \(\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = T\left( {60} \right) \Leftrightarrow k - 180 = 130 \Leftrightarrow k = 310\)
Vậy với \(k = 310\) thì hàm số \(T\left( t \right)\) liên tục trên tập xác định.

Số lượng tế bào đạt đến khối lượng Trái đất là: \(N = {6.10^{27}}{.10^3}:{5.10^{ - 13}} = 1,{2.10^{17}}\)
Số lần phân chia: \(N = {N_0}{.2^n} \Rightarrow n = \frac{{\lg N - \lg {N_0}}}{{\lg 2}} = \frac{{\lg 1,{{2.10}^{17}} - \lg {{5.10}^{ - 13}}}}{{\lg 2}} \approx 97,6\)
Thời gian cần thiết là; \(97,6:3 = 32,5\) (giờ)


Đổi 2 giờ 15 phút = \(\frac{9}{4}\)giờ.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là \(\frac{9}{4}.( - {360^ \circ }) = - {810^ \circ }\)