Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Các đường thẳng nối mỗi điểm A, B, C với bóng A', B', C' có đôi một song song.
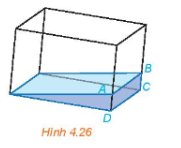
b) Để xác định được bóng đổ trên sàn nhà của mỗi điểm trên khung cửa sổ ta lấy một đường thẳng a cố định song song với ánh mặt trời.
Điểm O' là giao điểm của sàn nhà và đường thẳng đi qua O song song với a.
Tương tự, ta xác định được các điểm A', B', C', D'.

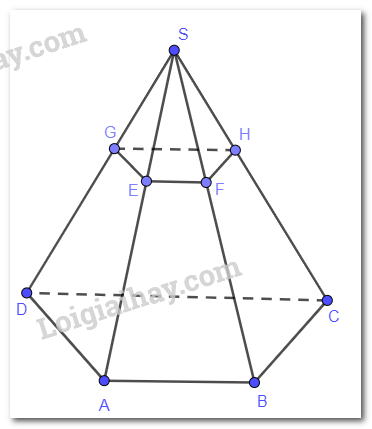
Mặt phẳng (SAD) chứa đường thẳng AD song song với mp(P) nên mặt phẳng (P) cắt (SAD) theo giao tuyến song song với AD. Vẽ EG // AD (G thuộc SD) thì EG là giao tuyến của (P) và (SAD).
Mặt phẳng (SAB) chứa đường thẳng AB song song với mp(P) nên mặt phẳng (P) cắt (SAB) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc SB) thì EF là giao tuyến của (P) và (SAB).
Ta có AB // CD, EF // AB suy ra CD // EF hay CD // mp(P)
Mặt phẳng (SCD) chứa đường thẳng CD song song với mp(P) nên mặt phẳng (P) cắt (SCD) theo giao tuyến song song với CD. Vẽ GH // CD (H thuộc SC) thì GH là giao tuyến của (P) và (SCD).
FH thuộc (P), FH thuộc (SBC) suy ra FH là giao tuyến của (P) và (SBC).
Tứ giác EFGH có EF // GH (vì cùng song song với CD) suy ra EFGH là hình thang.

Ta có: \(mp\left( {ABKI} \right) \cap mp\left( {CDIK} \right) = IK\)
\(mp\left( {ABKI} \right) \cap mp\left( {ABCD} \right) = AB\)
\(mp\left( {CDIK} \right) \cap \left( {ABCD} \right) = CD\)
Mà IK // CD (Do CDIK là hình chữ nhật) suy ra AB // CD.

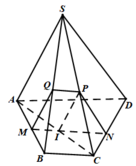
+ Ta tìm thiết diện của hình chóp cắt bởi (α):
Trong ( SAB) dựng MQ // SA( Q thuộc SB)
Gọi I là giao điểm của AC và MN.
Trong mp ( SAC); dựng IP// SA với P thuộc SC.
Khi dó thiết diện cần tìm là tứ giác MNPQ.
+ Tứ giác MNPQ là một hình thang khi MN// PQ hoặc MQ// PN.

=> MN//PQ nên tứ giác MNPQ là hình thang.
Vậy để tứ giác MNPQ là hình thang thì điều kiện là MN//BC.
Chọn C

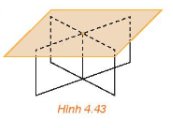
Do mặt bàn và mặt đất không có điểm chung nên chúng song song với nhau.

a: \(G\in\left(SCD\right);G\in\left(GAB\right)\)
Do đó: \(G\in\left(SCD\right)\cap\left(GAB\right)\)
Xét (SCD) và (GAB) có
\(G\in\left(SCD\right)\cap\left(GAB\right)\)
CD//AB
Do đó: (SCD) giao (GAB)=xy, xy đi qua G và xy//AB//CD

Tham khảo:
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng các mặt bên là hình tam giác
Hình thang ABCD có AB//CD và AB=2cm, CD=6cm nên hình biểu diễn của ABCD là một hình thang có đáy CD gấp ba đáy BC
Từ đó, ta vẽ được hình biểu diễn của S.ABCD.
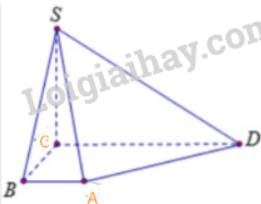

Ta có: SD và AB chéo nhau.
Vì AB và SD chéo nhau nên AB không nằm trong mp(SCD).
Vì AB // CD nên AB // mp(SCD).
Vậy (SCD) là mặt phẳng chứa SD và song song với AB.

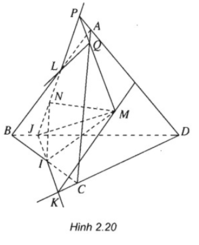
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
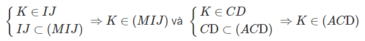
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
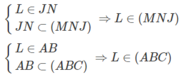
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
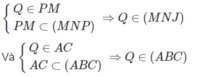
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).

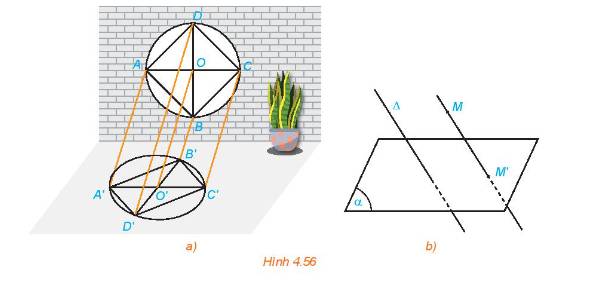
Vì các thanh chắn của chiếc thang song song với với nhau nên hình chiếu của chúng cũng song song với nhau.